题目内容
【题目】如图,O为坐标原点,四边彤OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,删△AOF的面积等于( )

A. 10 B. 9 C. 8 D. 6
【答案】A
【解析】 过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,设OA=a,BF=b,通过解直角三角形分别找出点A、F的坐标,结合反比例函数图象上点的坐标特征即可求出a、b的值,通过分割图形求面积,最终找出△AOF的面积等于梯形AMNF的面积,利用梯形的面积公式即可得出结论.
解:过点A作AM⊥x轴于点M,过点F作FN⊥x轴于点N,如图所示.
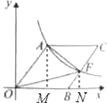
设OA=a,BF=b,
在Rt△OAM中,∠AMO=90°,OA=a,sin∠AOB=![]() ,
,
∴AM=OAsin∠AOB=![]() a,OM=
a,OM=![]() =
=![]() a,
a,
∴点A的坐标为(![]() a,
a, ![]() a).
a).
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴![]() a×
a×![]() a=
a=![]() a2=12,
a2=12,
解得:a=5,或a=﹣5(舍去).
∴AM=8,OM=6.
∵四边形OACB是菱形,
∴OA=OB=10,BC∥OA,
∴∠FBN=∠AOB.
在Rt△BNF中,BF=b,sin∠FBN=![]() ,∠BNF=90°,
,∠BNF=90°,
∴FN=BFsin∠FBN=![]() b,BN=
b,BN=![]() =
=![]() b,
b,
∴点F的坐标为(10+![]() b,
b, ![]() b).
b).
∵点F在反比例函数y=![]() 的图象上,
的图象上,
∴(10+![]() b)×
b)×![]() b=12,
b=12,
S△AOF=S△AOM+S梯形AMNF﹣S△OFN=S梯形AMNF=10
故选A.
“点睛”本题主要考查了菱形的性质、解直角三角形以及反比例函数图象上点的坐标特征,解题的关键是找出S△AOF=![]() S菱形OBCA.
S菱形OBCA.

练习册系列答案
相关题目