题目内容
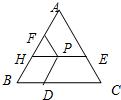 13、如图所示,△ABC为等边三角形,P是△ABC内任一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=
13、如图所示,△ABC为等边三角形,P是△ABC内任一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=4
.分析:PD∥AB,可把PD转化为BH,同样把PF转化为PH,PE与PF的和即为线段HE,又△AHE也是等边三角形,再把HE转化为AH,进而可求解PD+PE+PF的和.
解答:解:∵△ABC为等边三角形,PD∥AB,PE∥BC,PF∥AC,
∴△PHF为等边三角形,∴PF=PH,PD=BH,
又△AHE为等边三角形,∴HE=AH,
∴PD+PE+PF=BH+PE+PH=BH+HE=BH+AH=AB
△ABC的周长为12
∴AB=4,∴PD+PE+PF=4.
故填4.
∴△PHF为等边三角形,∴PF=PH,PD=BH,
又△AHE为等边三角形,∴HE=AH,
∴PD+PE+PF=BH+PE+PH=BH+HE=BH+AH=AB
△ABC的周长为12
∴AB=4,∴PD+PE+PF=4.
故填4.
点评:本题考查了平行四边形的判定和性质以及等边三角形的性质,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
相关题目
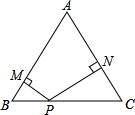 如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )
如图所示,△ABC为正三角形,P是BC上的一点,PM⊥AB,PN⊥AC,设四边形AMPN,△ABC的周长分别为m、n,则有( )A、
| ||||||
B、
| ||||||
C、80%<
| ||||||
D、78%<
|
 AE=120°,试问:
AE=120°,试问: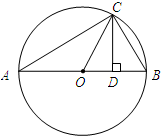 附加题.观察计算
附加题.观察计算 如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分.
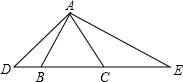
如图所示,△ABC为直角三角形,∠ACB=90°,BF平分∠ABC,CD⊥AB于D,CD交BF于点G,GE∥CA,求证:CE与FG互相垂直平分. 如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=
如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=