题目内容
在矩形ABCD中,对角线AC,BD交于点O,AB=6cm,AC=8cm.
(1)求BC的长;
(2)画出△AOB沿射线AD方向平移所得的△DEC;
(3)连接OE,写出OE与DC的关系?说明理由.

(1)求BC的长;
(2)画出△AOB沿射线AD方向平移所得的△DEC;
(3)连接OE,写出OE与DC的关系?说明理由.

(1)∵矩形ABCD,
∴∠CBA=90°,
AB=6cm,AC=8cm,由勾股定理:BC=
=
=2
(cm),
答:BC的长是2
cm.
(2)如图所示
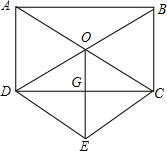
(3)答:OE与DC的关系是互相垂直平分.
理由是:∵矩形ABCD,
∴OA=OC,OD=OB,AC=BD,
∴OA=OC=OD=OB,
∵△AOB沿射线AD方向平移所得的△DEC,
∴OD=OC=DE=CE,
∴四边形ODEC是菱形,
∴OE⊥CD,OG=EG,CG=DG,
即OE与DC的关系是互相垂直平分.
∴∠CBA=90°,
AB=6cm,AC=8cm,由勾股定理:BC=
| AC2-AB2 |
| 82-62 |
| 7 |
答:BC的长是2
| 7 |
(2)如图所示

(3)答:OE与DC的关系是互相垂直平分.
理由是:∵矩形ABCD,
∴OA=OC,OD=OB,AC=BD,
∴OA=OC=OD=OB,
∵△AOB沿射线AD方向平移所得的△DEC,
∴OD=OC=DE=CE,
∴四边形ODEC是菱形,
∴OE⊥CD,OG=EG,CG=DG,
即OE与DC的关系是互相垂直平分.

练习册系列答案
相关题目




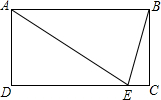
 AB=
AB=
