Question

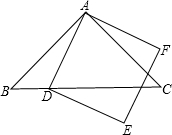如图所示，四边形ADEF为正方形，ABC为等腰直角三角形，D在BC边上，△ABC的面积等于98，BD：DC=2：5．则正方形ADEF的面积等于

 

．

Answer 1

分析：要求正方形ABCD的面积，求出边AD即可，求AD就要构建直角三角形，使得AD成为直角三角形的一边，故作辅助线AH．

解答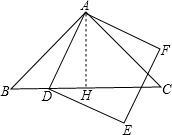：解：∵等腰直角△ABC的面积等于98，∴AB=AC=

98×2

=14，
故BC=14

2

，又∵BD：DC=2：5
∴DH=

1.5

7

× 14

2

=3

2

，AH=HC=

1

2

×14

2

=7

2

，
∴AD=

(3 2 )2+(7 2 )2

=

116

，
∴正方形ABCD的面积为S=AD²=116．
故本题答案为 116．

点评：本题考查了正方形四边均相等的性质，考查了等腰直角三角形高和斜边的关系，本题的关键是构建直角三角形，使得AD成为直角三角形的一边．