题目内容
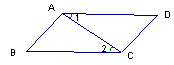
如图所示在四边形ABCD中，∠ADC=∠BCD＞90°，AC与BD交于P点，过A作AF∥BC交BD延长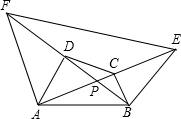
线于F，过B作BE∥AD交AC延长线于E．求证：（1）PE=
| PA•PB | PD |
（2）CD∥EF．
分析：（1）根据相似三角形的判定以及相似三角形的相似比相等的性质即可证明；
（2）根据相似三角形的判定以及相似三角形的比例关系，再结合（1）中的结论即可证明CD∥EF．
（2）根据相似三角形的判定以及相似三角形的比例关系，再结合（1）中的结论即可证明CD∥EF．
解答：证明：（1）∵AD∥BE，
∴△PAD∽△PEB，
∴
=
，
∴PE=
；
（2）∵BC∥AF，
∴△PBC∽△PFA，
∴
=
，
∴PF=
，
结合①得
=
，
在△PEF中有CD∥EF．
∴△PAD∽△PEB，
∴
| PE |
| PA |
| PB |
| PD |
∴PE=
| PA•PB |
| PD |
（2）∵BC∥AF，
∴△PBC∽△PFA，
∴
| PF |
| PB |
| PA |
| PC |
∴PF=
| PA•PB |
| PC |
结合①得
| PE |
| PF |
| PC |
| PD |
在△PEF中有CD∥EF．
点评：本题主要考查了相似三角形的判定及性质，难度适中．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
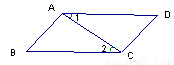
如图所示,在四边形ABCD中，AD∥BC,要使四边形ABCD成为平行四边形还需要条件( )
| A．AB="DC" | B．∠1="∠2" | C．AB="AD" | D．∠D=∠B |