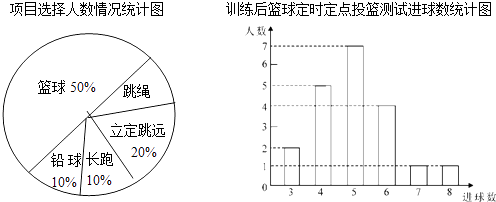
题目内容
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC,∠EAC=90°,点M为射线AE上任意一点(不与点A重合),连接CM,将线段CM绕点C按顺时针方向旋转90°得到线段CN,直线NB分别交直线CM,射线AE于点F、D.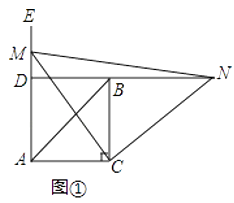
(1)问题发现:直接写出∠NDE=度;
(2)拓展探究:试判断,如图②当∠EAC为钝角时,其他条件不变,∠NDE的大小有无变化?请给出证明.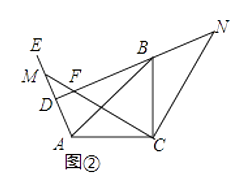
(3)如图③,若∠EAC=15°,BD= ![]() ,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.
,直线CM与AB交于点G,其他条件不变,请直接写出AC的长.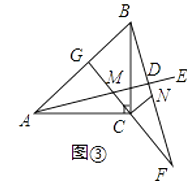
【答案】
(1)90
(2)解:∠NDE的大小不变,
在△MAC和△NBC中,
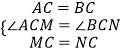 ,
,
∴△MAC≌△NBC,
∴∠N=∠AMC,
又∵∠MFD=∠NFC,
∴∠MDF=∠FCN=90°,
即∠NDE=90°
(3)解:AC=2,
在△MAC和△NBC中,
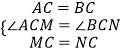 ,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=15°,
如图③,设BC与AD交于点H,
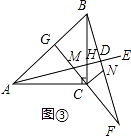
又∵∠AHC=∠BHD,
∴∠BDH=∠ACH=90°,
∴在Rt△ABD中,∠ABD=∠ABC+∠NBC=45°+15°=60°
∵BD= ![]() ,
,
∴AB=2 ![]() ,
,
∴AC=ABcos45°=2.
【解析】解:(1)∵∠ACB=90°,∠MCN=90°,
∴∠ACM=∠BCN,
在△MAC和△NBC中,
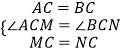 ,
,
∴△MAC≌△NBC,
∴∠NBC=∠MAC=90°,
又∵∠ACB=90°,∠EAC=90°,
∴∠NDE=90°.
所以答案是:90.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
【题目】某公司为了扩大经营,决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
甲 | 乙 | |
价格(万元/台) | 7 | 5 |
每台日产量(个) | 100 | 60 |
(1)按该公司要求可以有几种购买方案?
(2)如果该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择什么样的购买方案?