题目内容
【题目】已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为( )
A.![]()
B.![]()
C.![]()
D.2
【答案】D
【解析】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点C(﹣1,4),
如图所示,作CD⊥AB于D.
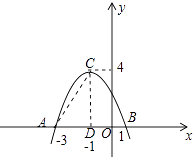
在RT△ACD中,tan∠CAD= ![]() =
= ![]() =2,
=2,
所以答案是D.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点和锐角三角函数的定义的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
【题目】为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
七年级(3)班学生到图书馆的次数统计表
到图书馆的 | 0次 | 1次 | 2次 | 3次 | 4次及 |
人数 | 5 | 10 | m | 8 | 12 |
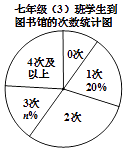
(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?