题目内容
如图1,在等腰梯形ABCO中,AB∥CO,E是AO的中点,过点E作EF∥OC交BC于F,AO=4,OC=6,∠AOC=60°.现把梯形ABCO放置在平面直角坐标系中,使点O与原点重合,OC在x轴正半轴上,点A,B在第一象限内.
(1)求点E的坐标及线段AB的长;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,连结PN,设PE=x.△PMN的面积为S.
①求S关于x的函数关系式;
②△PMN的面积是否存在最大值,若不存在,请说明理由.若存在,求出面积的最大值;

(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2).设运动时间为t秒,运动后的直角梯形为E′D′G′H′(如图3);试探究:在运动过程中,等腰梯ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式.
(1)求点E的坐标及线段AB的长;
(2)点P为线段EF上的一个动点,过点P作PM⊥EF交OC于点M,过M作MN∥AO交折线ABC于点N,连结PN,设PE=x.△PMN的面积为S.
①求S关于x的函数关系式;
②△PMN的面积是否存在最大值,若不存在,请说明理由.若存在,求出面积的最大值;

(3)另有一直角梯形EDGH(H在EF上,DG落在OC上,∠EDG=90°,且DG=3,HG∥BC.现在开始操作:固定等腰梯形ABCO,将直角梯形EDGH以每秒1个单位的速度沿OC方向向右移动,直到点D与点C重合时停止(如图2).设运动时间为t秒,运动后的直角梯形为E′D′G′H′(如图3);试探究:在运动过程中,等腰梯ABCO与直角梯形E′D′G′H′重合部分的面积y与时间t的函数关系式.
(1)E(1, ),AB=2(2)①
),AB=2(2)① ②
② (3)y=-
(3)y=- t+
t+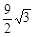 ,y=
,y= 
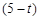 2
2
 ),AB=2(2)①
),AB=2(2)① ②
② (3)y=-
(3)y=- t+
t+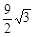 ,y=
,y= 
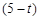 2
2解:(1)E(1, ),AB=2( 4分)
),AB=2( 4分)
(2)①当0≤x≤1时,S= ,当
,当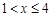 时,
时, (2分)
(2分)
②若0≤x≤1时,S=
若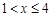 时,
时, ∵-
∵-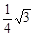 <0 ∴S随x的增大而减小∴S不存在最大值
<0 ∴S随x的增大而减小∴S不存在最大值
∴综上所述,当0≤x≤1时,S存在最大值,最大值为 (2分)
(2分)
(3)当0≤t≤2时,直角梯形E′D′G′H′落在等腰梯形内部,
这时重叠部分的面积即为直角梯形面积,y=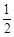 ×(2+3)×
×(2+3)× =
=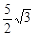
当2<t≤4时,y=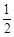 ×(4-t+5-t)×
×(4-t+5-t)× =-
=- t+
t+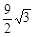
当4<t≤5时,y=(5-t)×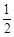 ×
× (5-t)=
(5-t)= 
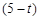 2(4分)
2(4分)
(1)过点E作OC的垂线EW,垂足为W,解直角三角形EOW可求得点E的坐标,
以及线段AB的值
(2)中利用线线平行和已知的AO=MN,求三角形PMN面积,只需要求解高即可,利用给出的x分类讨论,0≤x≤1和当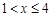 时点到两种不同的结果,然后根据得到的面积表达式为二次函数,利用二次函数的性质得到最值。
时点到两种不同的结果,然后根据得到的面积表达式为二次函数,利用二次函数的性质得到最值。
(3)根据梯形运行的时间可知,求解的面积公式需要分类讨论。当0≤t≤2时,直角梯形E′D′G′H′落在等腰梯形内部,这时重叠部分的面积即为直角梯形面积
当2<t≤4时,和当4<t≤5时,结合梯形面积公式得到结论。
 ),AB=2( 4分)
),AB=2( 4分)(2)①当0≤x≤1时,S=
 ,当
,当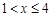 时,
时, (2分)
(2分)②若0≤x≤1时,S=

若
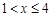 时,
时, ∵-
∵-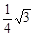 <0 ∴S随x的增大而减小∴S不存在最大值
<0 ∴S随x的增大而减小∴S不存在最大值 ∴综上所述,当0≤x≤1时,S存在最大值,最大值为
 (2分)
(2分)(3)当0≤t≤2时,直角梯形E′D′G′H′落在等腰梯形内部,
这时重叠部分的面积即为直角梯形面积,y=
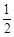 ×(2+3)×
×(2+3)× =
=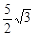
当2<t≤4时,y=
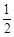 ×(4-t+5-t)×
×(4-t+5-t)× =-
=- t+
t+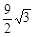
当4<t≤5时,y=(5-t)×
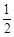 ×
× (5-t)=
(5-t)= 
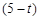 2(4分)
2(4分)(1)过点E作OC的垂线EW,垂足为W,解直角三角形EOW可求得点E的坐标,
以及线段AB的值
(2)中利用线线平行和已知的AO=MN,求三角形PMN面积,只需要求解高即可,利用给出的x分类讨论,0≤x≤1和当
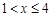 时点到两种不同的结果,然后根据得到的面积表达式为二次函数,利用二次函数的性质得到最值。
时点到两种不同的结果,然后根据得到的面积表达式为二次函数,利用二次函数的性质得到最值。(3)根据梯形运行的时间可知,求解的面积公式需要分类讨论。当0≤t≤2时,直角梯形E′D′G′H′落在等腰梯形内部,这时重叠部分的面积即为直角梯形面积
当2<t≤4时,和当4<t≤5时,结合梯形面积公式得到结论。

练习册系列答案
相关题目

 千米时(t≥30),求他们经过的时间t的取值范围
千米时(t≥30),求他们经过的时间t的取值范围
 路线运动,到D停止;点
路线运动,到D停止;点 从
从 出发,沿
出发,沿 路线运动,到
路线运动,到 停止.若点
停止.若点
 的速度为
的速度为 点
点 ,
, 秒时点
秒时点 .图②是点
.图②是点 的面积
的面积 与
与 的函数关系图象;图③点
的函数关系图象;图③点 秒后
秒后 的面积
的面积 的函数关系图象.
的函数关系图象. 、c的值及点
、c的值及点 的值;
的值; 点
点 请分别写出动点
请分别写出动点 改变速度后
改变速度后 与出发后的运动时间
与出发后的运动时间
 时,直接写出∠DEF的度数;
时,直接写出∠DEF的度数; ,∠DEF=
,∠DEF= (
( <X<
<X< ,
,
 的图象不经过
的图象不经过