Question

【题目】探究

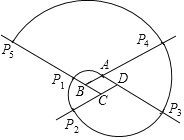
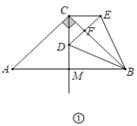
（1）如图①，在等腰直角三角形中，，作交于点，点为射线上一点，以点为旋转中心将线段逆时针旋转90°得到线段，连接交射线于点，连接、．

　　　　　　　　

填空：

①线段、的数量关系为___________．

②线段、的位置关系为___________．

推广：

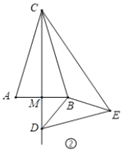
（2）如图②，在等腰三角形中，，作交于点，点为外部射线上一点，以点为旋转中心将线段逆时针旋转度得到线段，连接、、请判断（1）中的结论是否成立，并说明理由．

应用：

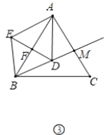
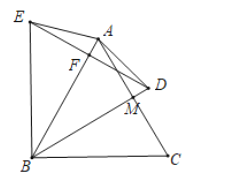
（3）如图③，在等边三角形中，．作交于点，点为射线上一点，以点为旋转中心将线段逆时针旋转60°得到线段，连接交射线于点，连接、．当以、、为顶点的三角形与全等时，请直接写出的值．

Answer 1

【答案】(1) BD=BE, BC⊥DE；(2) 结论：（1）中的结论仍然成立,理由见解析；（3）或或4．

【解析】

(1)如图①中，只要证明△CBD≌△CBE（SAS），再运用全等三角形的性质即可；

（2）结论不变。如图②中，只要证明△CBD≌△CBE（SAS），再运用全等三角形的性质即可；

（3）分点D在线段BM上和点D在线段BM的延长线上两种情形分别求解即可．

解：（1）如图①，

∵CA=CB，∠ACB=90°，CM平分∠ACB，

∴∠ACM=∠BCM=45°，

∵∠ECD=90°，

∴∠ECF=∠DCF=45°， CD=CE CB=CB

∴△CBD≌△CBE（SAS），

∴BD=BE，

∴CD=CE

∴BC垂直平分线段DE，

∴BC⊥DE.

故答案为BD=BE, BC⊥DE；

(2)结论：（1）中的结论仍然成立;理由：如图②，

∴CA=CB，∠ACB= ,CM平分∠ACB

∴∠ACM=∠BCM=，

∵∠ECD=，

∴∠ECF=∠DCF=,

∵CD=CE, CB=CB

∴△CBD≌△CBF（SAS）

∴BD=BE

∴CD=CE，

∵BC垂直平分线段DE，

∴BC⊥DE

(3) 当点D在线段BM上时，即△AFE≌△AMD时，AF=AM，

∵∠AFD=∠AMD=90°AD=AD,

∴Rt△ADF≌Rt△ADM（HL）

∴∠DAF=∠DAM=30°

∴∠DBA=∠DAB=30°

∴DA=DB

∵DF⊥AB

∴∠BDF=60°，BF=AF=2

BD=BE

∴△BDE是等边三角形，

∴DF=EF= BF·tan30°=

DE=2EF=

如图③-1中，当点D在BM的延长线时，易证AF=AM=2，DE=2DF=

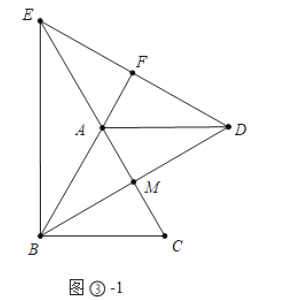
如图③-2中，当EF=AM=DF时，也满足条件，此时DE=BD=AB=4，

综上所述，满足条件的DE的值为或或4．