题目内容
【题目】冬天来了,晒衣服成了头疼的事情,聪明的小华想到一个好办法,在家后院地面(BD)上立两根等长的立柱AB、CD(均与地面垂直),并在立柱之间悬挂一根绳子.绳子的形状近似成了抛物线![]() ,如图1,已知BD=8米,绳子最低点离地面的距离为1米.
,如图1,已知BD=8米,绳子最低点离地面的距离为1米.
(1)求立柱AB的长度;
(2)由于挂的衣服比较多,为了防止衣服碰到地面,小华用一根垂直于地面的立柱MN撑起绳子(如图2),MN的长度为1.85米,通过调整MN的位置,使左边抛物线F1对应函数的二次项系数为![]() ,顶点离地面1.6米,求MN离AB的距离.
,顶点离地面1.6米,求MN离AB的距离.
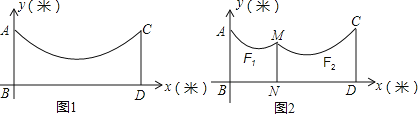
【答案】(1)AB=2.6米;(2)MN与AB的距离为3米.
【解析】试题分析:(1)由题意可得抛物线顶点坐标为(4,1),所以抛物线解析式为y=![]() (x-4)2+1,要求AB的长度,令x=0即可,求出函数值即可;(2)首先根据题意设出抛物线F1的解析式为y=
(x-4)2+1,要求AB的长度,令x=0即可,求出函数值即可;(2)首先根据题意设出抛物线F1的解析式为y=![]() (x+h)2+1.6,再将A的坐标代入函数解析式即可求出h,最后令y=1.85,解出x即可求出MN离AB的距离.
(x+h)2+1.6,再将A的坐标代入函数解析式即可求出h,最后令y=1.85,解出x即可求出MN离AB的距离.
试题解析:
(1)由题意得,抛物线顶点坐标为(4,1),
所以抛物线解析式为:y=![]() (x-4)2+1,
(x-4)2+1,
令x=0,y=![]() ×16+1=2.6.
×16+1=2.6.
所以AB=2.6;
(2)设抛物线F1解析式为:y=![]() (x+h)2+1.6,
(x+h)2+1.6,
∵A(0,2.6),
∴2.6=![]() h2+1.6,
h2+1.6,
解得h=±2,正值舍去,
∴h=-2,
∴F1解析式为:y=![]() (x-2)2+1.6,
(x-2)2+1.6,
令y=1.85,1.85=![]() (x-2)2+1.6,
(x-2)2+1.6,
解得x1=1(舍去),x2=3,
所以MN与AB的距离为3米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目