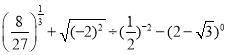题目内容
【题目】如图，已知AD⊥BC，垂足为点D，EF⊥BC，垂足为点F，∠1+∠2=180°．请填写∠CGD=∠CAB的理由．
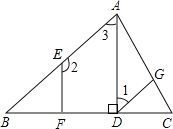
解：因为AD⊥BC，EF⊥BC（______ ）
所以∠ADC=90°，∠EFD=90°（______ ）
得∠ADC=∠EFD（等量代换），
所以AD∥EF（______ ）
得∠2+∠3=180°（______ ）
由∠1+∠2=180°（______ ）
得∠1=∠3（______ ）
所以DG∥AB（______ ）
所以∠CGD=∠CAB（______ ）
【答案】已知 垂直定义 同位角相等，两直线平行 两直线平行，同旁内角互补 已知 同角的补角相等 内错角相等，两直线平行 两直线平行，同位角相等
【解析】
求出AD∥EF，根据平行线的性质得出∠2+∠3=180°，求出∠1=∠3，根据平行线的判定得出DG∥AB，根据平行线的性质得出∠CGD=∠CAB即可．
解：∵AD⊥BC，EF⊥BC（已知），
∴∠ADC=90°，∠EFC=90°（垂直定义），
∴∠ADC=∠EFD，
∴AD∥EF（同位角相等，两直线平行），
∴∠2+∠3=180°（两直线平行，同旁内角互补），
∵∠1+∠2=180°（已知），
∴∠1=∠3（同角的补角相等），
∴DG∥AB（内错角相等，两直线平行），
∴∠CGD=∠CAB（两直线平行，同位角相等）．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
