题目内容
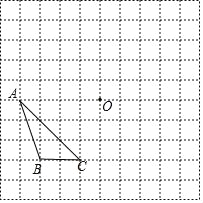
【题目】如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A,B,C及点O均在格点上请按要求完成以下操作或运算:
(1)将△ABC绕点O旋转90°,得到△A1B1C1;
(2)求点B旋转到点B1的路径长(结果保留π).
【答案】(1)见解析;(2)![]()
【解析】
(1)依据旋转中心、旋转方向和旋转角度,即可得到△A1B1C1;
(2)利用扇形弧长计算公式进行计算,即可得到点B旋转到点B1的路径长.
解:(1)若△ABC绕点O顺时针旋转90°,可得△A1B1C1,如图所示:

若△ABC绕点O逆时针旋转90°,可得△A1B1C1,如图所示:

(2)若△ABC绕点O顺时针旋转90°,点B旋转到点B1的路径长为![]() =
=![]() ;
;
若△ABC绕点O逆时针旋转90°,同理可得点B旋转到点B1的路径长为![]() .
.

练习册系列答案
相关题目
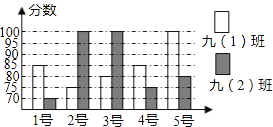
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.