题目内容
 如图,A、P、B、C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于Q点.
如图,A、P、B、C是⊙O上的四点,∠APC=∠BPC=60°,AB与PC交于Q点.
(1)判断△ABC的形状,并证明你的结论;
(2)求证: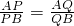 ;
;
(3)若∠ABP=15°,△ABC的面积为4 ,求PC的长.
,求PC的长.
 (1)解:△ABC是等边三角形.
(1)解:△ABC是等边三角形.证明:∵∠ABC=∠APC=60°,∠BAC=∠BPC=60°,
∴∠ACB=180°-∠ABC-∠BAC=60°,
∴△ABC是等边三角形;
(2)证明:如图,过B作BD∥PA交PC于D,则∠BDP=∠APC=60°,
又∵∠AQP=∠BQD,

∴△AQP∽△BQD,
∴
 ,
,∵∠BPD=∠BDP=60°,
∴PB=BD,
∴
 ;
;(3)解:设正△ABC的高为h,则h=BC•sin60°.
∵
 BC•h=4
BC•h=4 ,
,即
 BC•BC•sin60°=4
BC•BC•sin60°=4 ,
,解得BC=4,
连接OB,OC,OP,作OE⊥BC于E,
由△ABC是正三角形知∠BOC=120°,从而得∠OCE=30°,
∴
 ,
,由∠ABP=15°得∠PBC=∠ABC+∠ABP=75°,
于是∠POC=2∠PBC=150°,

∴∠PCO=(180°-150°)÷2=15°,
如图,作等腰直角△RMN,在直角边RM上取点G,使∠GNM=15°,则∠RNG=30°,
作GH⊥RN,垂足为H.
设GH=1,则cos∠GNM=cos15°=
 .
.在Rt△GHN中,

NH=GN•cos30°,GH=GN•sin30°,
∴RH=GH,MN=RN•sin45°,
∴cos15°=
 .
.在图中,作OF⊥PC于F,
∴PC=2CF=2OC•cos15°=
 .
.分析:(1)由圆周角定理知,∠BAC=∠BPC=∠APC=∠BPC=60°,即可证明△ABC是等边三角形;
(2)过B作BD∥PA交PC于D,证得△AQP∽△BQD,
 ,再证PB=BD即可;
,再证PB=BD即可;(3)通过作辅助线,构造等腰直角三角形求解.
点评:本题利用了圆周角定理,等边三角形的判定和性质,锐角三角函数的概念,三角形的面积公式,等腰直角三角形的性质,通过作辅助线,构造相似三角形和等腰直角三角形求解,有很强的综合性.

练习册系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.