题目内容
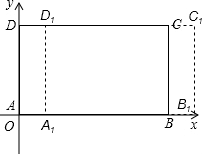
在长方形ABCD中,AB=20cm,BC=12cm.
(1)以A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,并写A、B、C、D的坐标;
(2)若此长方形以每秒2cm的速度沿x轴正方向移动2秒后,直接写出对应点A1B1C1D1的坐标;
(3)经过多长时间,平移后后的长方形与原来长方形重叠部分面积为24平方厘米.
(1)以A为原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,并写A、B、C、D的坐标;
(2)若此长方形以每秒2cm的速度沿x轴正方向移动2秒后,直接写出对应点A1B1C1D1的坐标;
(3)经过多长时间,平移后后的长方形与原来长方形重叠部分面积为24平方厘米.
(1)如图,A(0,0),B(20,0),C(20,12),D(0,12);
(2)2×2=4cm,
所以,A1(4,0),B1(24,0),C1(24,12),D1(4,12);
(3)平移后重叠部分的矩形的长为24÷12=2cm,
所以,平移距离为20-2=18cm,
时间=18÷2=9秒.
(2)2×2=4cm,
所以,A1(4,0),B1(24,0),C1(24,12),D1(4,12);
(3)平移后重叠部分的矩形的长为24÷12=2cm,
所以,平移距离为20-2=18cm,
时间=18÷2=9秒.


练习册系列答案
相关题目