题目内容
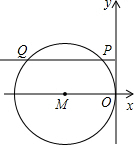
如图，在平面直角坐标系中，⊙M与y轴相切于原点O，平行与x轴的直线交⊙M于P，Q两点，点P在点Q的右侧，若点P的坐标是（-1，2），则弦QP的长是______．
过点M作直线PQ的垂线，垂足为N，连接MP，
设PN=a，由垂径定理可知，QP=2PN=2a，
在直角△MNP中，MP=MO=a+1，MN=2，
由勾股定理得：MN2+NP2=MP2，即22+a2=（a+1）2，
解得a=
，
即QP=3．
故答案为：3．
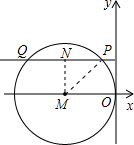
设PN=a，由垂径定理可知，QP=2PN=2a，
在直角△MNP中，MP=MO=a+1，MN=2，
由勾股定理得：MN2+NP2=MP2，即22+a2=（a+1）2，
解得a=
| 3 |
| 2 |
即QP=3．
故答案为：3．
练习册系列答案
高中必刷题系列答案
相关题目
