题目内容
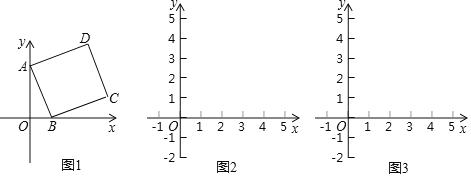
【题目】利用图形面积可以解释代数恒等式的正确性,如图1可以验证一个代数恒等式(a+b)2=(a﹣b)2+4ab.
(1)如图2,用若干张A,B,C的卡片拼成一个长方形面积为(2a+b)(a+b),那么需要A,B,C卡片各多少张?
(2)如果用1张A,5张B,6张C拼成一个长方形,那么这个长方形的边长分别是 和 .

【答案】(1)需要A卡片2张,B卡片3张,C卡片1张;(2)(a+2b);(a+3b).
【解析】
(1)按照多项式乘法的运算法则将(2a+b)(a+b)展开,则可得需要的A,B,C纸片的张数;
(2)先算出用1张A,5张B,6张C拼成一个长方形的面积,再将其因式分解,则可得这个长方形的边长.
(1)∵(2a+b)(a+b)=2a2+3ab+b2
而图片A,B,C的面积分别为:a2,ab,b2
∴需要A卡片2张,B卡片3张,C卡片1张.
(2)如果用1张A,5张B,6张C拼成一个长方形
则其面积为:a2+5ab+6b2;
∵a2+5ab+6b2=(a+2b)(a+3b)
∴这个长方形的边长分别是(a+2b)和(a+3b).
故答案为:(a+2b);(a+3b).

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目