题目内容
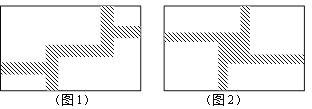
【题目】(1)如图1,在一块宽为12m,长为20m的矩形地面上修筑同样宽的道路,余下的部分种上草坪.要使草坪的面积为180m2,求道路的宽;
(2)现在对该矩形区域进行改造,如图2,在正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四边连接四条与矩形的边互相平行的且宽度相等的道路,已知道路的宽为正方形边长的![]() .若道路与观赏亭的面积之和是矩形面积的
.若道路与观赏亭的面积之和是矩形面积的![]() ,求道路的宽.
,求道路的宽.
【答案】(1)道路宽为2米;(2)道路的宽为1米.
【解析】试题分析:(1)设道路宽为x米,利用平移把不规则的图形变为规则图形,如此一来,所有草坪面积之和就变为了(20﹣x)(12﹣x)米2,进而即可列出方程,求出答案;
(2)设道路的宽为x米,则正方形边长为4x,根据道路与观赏亭的面积之和是矩形面积的![]() ,列方程求解即可.
,列方程求解即可.
试题解析:解:(1)设道路宽为x米,
根据题意得:(20﹣x)(12﹣x)=180
解得:x1=30(舍去),x2=2
答:道路宽为2米;
(2)设道路的宽为x米,
则可列方程:x(12-4x)+x(20-4x)+16x2=![]() ×20×12,
×20×12,
即:x2+4x-5=0,
解得:x1=1,x2=-5(舍去),
答:道路的宽为1米.
点睛:考查了一元二次方程的应用,这类题目体现了数形结合的思想,需利用平移把不规则的图形变为规则图形,进而即可列出方程,求出答案.另外还要注意解的合理性,从而确定取舍.
【题型】解答题
【结束】
10
【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
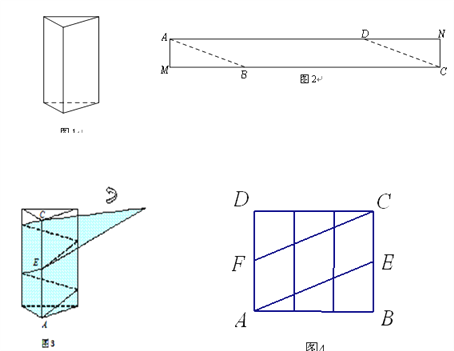
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数).
【答案】(1)作图见解析;(2)∠ABM=30°.
【解析】分析:(1)将图4中的△ABE向左平移30cm,△CDF向右平移30cm,拼成如图中的平行四边形,此平行四边形即为图2中的四边形ABCD.
(2)根据题意先求得AB=30cm,由纸带的宽为15cm,根据三角函数求得∠AMB=30°.
本题解析:(1)如图:
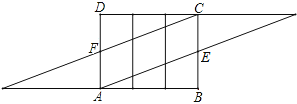
(2)由图2的包贴方法知:AB的长等于三棱柱的底边周长,∴AB=30.
∵ 纸带宽为15,∴ sin∠ABM =![]() .∴∠AMB=30°.
.∴∠AMB=30°.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案