题目内容
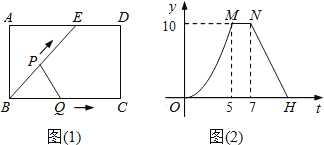
【题目】两个反比例函数y= 
（k＞1）和y= 
在第一象限内的图象如图所示，点P在y= 的图象上，PC⊥x轴于点C，交y= 的图象于点A，PD⊥y轴于点D，交y= 的图象于点B，BE⊥x轴于点E，当点P在y= 图象上运动时，以下结论：①BA与DC始终平行；②PA与PB始终相等；③四边形PAOB的面积不会发生变化；④△OBA的面积等于四边形ACEB的面积．其中一定正确的是（填序号） 
【答案】①③④
【解析】解：设点P的坐标为（m， 
），则点A（m， 
），点C（m，0），点B（ 
， ），点D（0， ）， ∴PB=m﹣ = 
，PD=m，PA= ﹣ = 
，PD=m，PC= ，
∵ 
= ， 
= = ，
∴BA∥DC，①成立；
∵PB= ，PA= ，
∴当m2=k时，PA=PB，②不成立；
S矩形OCPD=k，S△OBD= 
，S△OAC= ，
S四边形PAOB=S矩形OCPD﹣S△OBD﹣S△OBD=k﹣1，
∵k为固定值，
∴③成立；
S梯形BECA= （AC+BE）EC= （ + ）（m﹣ ）= 
，S△OBA=S四边形PAOB﹣S△PAB=k﹣1﹣ （m﹣ ）（ ﹣ ）= ，
∴S梯形BECA=S△OBA ， ④成立．
综上可知：一定正确的为①③④．
所以答案是：①③④．
【考点精析】本题主要考查了反比例函数的性质和比例系数k的几何意义的相关知识点，需要掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大；几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题．
