Question

【题目】如图，Rt△ABC的顶点B在反比例函数 的图象上，AC边在x轴上，已知∠ACB=90°，∠A=30°，BC=4，则图中阴影部分的面积是（ ）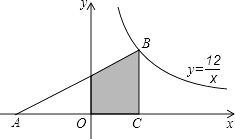
A.12
B.4
C.12-3
D.

Answer 1

【答案】D
【解析】解：∵∠ACB=90°，BC=4， ∴B点纵坐标为4，
∵点B在反比例函数 的图象上，
∴当y=4时，x=3，即B点坐标为（3，4），
∴OC=3．
在Rt△ABC中，∠ACB=90°，∠A=30°，BC=4，
∴AB=2BC=8，AC= BC=4 ，OA=AC﹣OC=4 ﹣3．
设AB与y轴交于点D．
∵OD∥BC，
∴ ，即 = ，
解得OD=4﹣ ，
∴阴影部分的面积是： （OD+BC）OC= （4﹣ +4）×3=12﹣ ．
故选：D．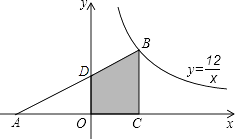

先由∠ACB=90°，BC=4，得出B点纵坐标为4，根据点B在反比例函数 的图象上，求出B点坐标为（3，4），则OC=3，再解Rt△ABC，得出AC=4 ，则OA=4 ﹣3．设AB与y轴交于点D，由OD∥BC，根据平行线分线段成比例定理得出 ，求得OD=4﹣ ，最后根据梯形的面积公式即可求出阴影部分的面积．