题目内容
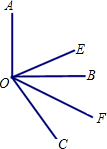 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.(1)求∠EOF的度数;
(2)若∠AOC=x°,∠EOF=y°.则请用x的代数式来表示y;
(3)如果∠AOC+∠EOF=156°,则∠EOF是多少度?
分析:(1)先求出∠AOC的度数,再根据角平分线的定义求出∠EOC与∠COF的度数,然后相减即可得解;
(2)先求出∠BOC的度数,再根据角平分线的定义求出∠COF与∠EOC,然后根据∠EOF=∠EOC-∠COF列式整理即可;
(3)根据(2)的规律,∠EOF的度数等于∠AOB的一半,进行求解即可.
(2)先求出∠BOC的度数,再根据角平分线的定义求出∠COF与∠EOC,然后根据∠EOF=∠EOC-∠COF列式整理即可;
(3)根据(2)的规律,∠EOF的度数等于∠AOB的一半,进行求解即可.
解答:解:(1)∵∠AOB是直角,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=90°+60°=150°,
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=
∠AOC=
×150°=75°,
∠COF=
∠BOC=
×60°=30°,
∴∠EOF=∠EOC-∠COF=75°-30°=45°;
(2)∵∠AOB是直角,∠AOC=x°,
∴∠BOC=∠AOC-∠AOB=x°-90°,
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=
∠AOC=
x°,
∠COF=
∠BOC=
(x°-90°),
∴∠EOF=∠EOC-∠COF=
x°-
(x°-90°)=45°;
(3)根据(2)的规律发现,∠EOF的度数只与∠AOB有关,
∠EOF=
∠AOB=
×90°=45°.
∴∠AOC=∠AOB+∠BOC=90°+60°=150°,
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠EOC-∠COF=75°-30°=45°;
(2)∵∠AOB是直角,∠AOC=x°,
∴∠BOC=∠AOC-∠AOB=x°-90°,
∵OE平分∠AOC,OF平分∠BOC,
∴∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EOF=∠EOC-∠COF=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据(2)的规律发现,∠EOF的度数只与∠AOB有关,
∠EOF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了角的计算,主要利用了角的平分线的定义,对识图能力有一定要求,快速准确识图是解题的关键.

练习册系列答案
相关题目
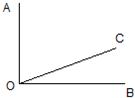 17、如图,已知∠AOB是直角,∠AOC是∠COB的3倍,则∠COB是
17、如图,已知∠AOB是直角,∠AOC是∠COB的3倍,则∠COB是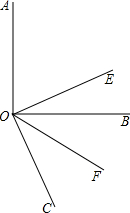 如图,已知∠AOB是直角,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,OE平分∠AOC,OF平分∠BOC.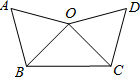 8、如图,已知△AOB是正三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )
8、如图,已知△AOB是正三角形,OC⊥OB,OC=OB,将△OAB绕点O按逆时针方向旋转,使得OA与OC重合,得到△OCD,则旋转的角度是( )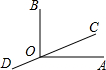 (1997•西宁)如图,已知∠AOB是直角,C、O、D三点共线,∠AOC=25°,则∠AOC的余角的补角为
(1997•西宁)如图,已知∠AOB是直角,C、O、D三点共线,∠AOC=25°,则∠AOC的余角的补角为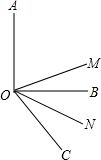 如图,已知∠AOB是直角,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB是直角,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.