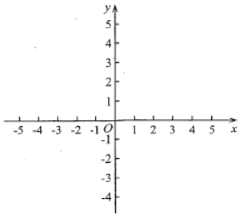
��Ŀ����
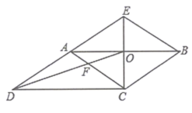
����Ŀ����֪����ABC�У�AC��BC��m��D��AB���ϵ�һ�㣬����B���Ź���D��ֱ���۵���ʹ��B����AC�ߵĵ�P���������A��C�غϣ����ۺ۽�BC���ڵ�E��
��1��������֪ ��ͼ1������C��60����D��AB���е㣬��֤��AP��![]() AC��
AC��
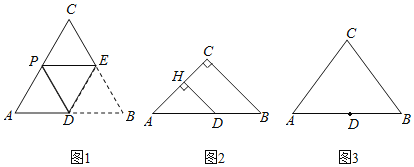
��2����ʽ���� ��ͼ2������C��90����m��6![]() ��AD��7������D��DH��AC�ڵ�H����DH��AP�ij���
��AD��7������D��DH��AC�ڵ�H����DH��AP�ij���
��3������̽�� ��ͼ3����m��10��AB��12���ҵ�AD��aʱ���������β�ͬ���۵���ʹ��B����AC����������ͬ��λ�ã���ֱ��д��a��ȡֵ��Χ��
���𰸡���1��֤������������2��![]() ��4
��4![]() ��3
��3![]() ����3��6��a��
����3��6��a��![]() .
.
��������
��1�����ݵȱ������ε����ʣ����õȱ��������ڽǶ�Ϊ60���Լ�������Ƚ�����⣮
��2���������������ε����ʣ����ö�Ӧ�߳ɱ����Լ����ɶ���������⣮
��3���������Ǻ����Լ����ߺ�һ���ʣ����ù��ɶ����Լ�������ϵ������⣮
��1��֤������AC��BC����C��60����
���ABC�ǵȱ������Σ�
��AC��AB����A��60����
�����⣬��DB��DP��DA��DB��
��DA��DP��
���ADPʹ�õȱ������Σ�
��AP��AD��![]() AB��
AB��![]() AC��
AC��
��2���⣺��AC��BC��6![]() ����C��90����
����C��90����
��AB��![]() ��
��![]() ��12��
��12��
��DH��AC��
��DH��BC��
���ADH�ס�ABC��
��![]() ��
��![]() ��
��
��AD��7��
��![]() ��
��![]() ��
��
��DH��![]() ��
��
����B�ع���D��ֱ���۵���
����һ������B�����߶�CH�ϵĵ�P1��ʱ����ͼ2��1�У�
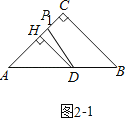
��AB��12��
��DP1��DB��AB��AD��5��
��HP1��![]() ��
��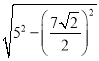 ��
��![]() ��
��
��A1��AH+HP1��4![]() ��
��
���ζ�������B�����߶�AH�ϵĵ�P2��ʱ����ͼ2��2�У�
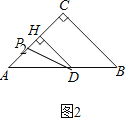
ͬ����֤HP2��![]() ��
��
��AP2��AH��HP2��3![]() ��
��
��������������������AP��ֵΪ4![]() ��3
��3![]() ��
��
��3����ͼ3�У�����C��CH��AB��H������D��DP��AC��P��
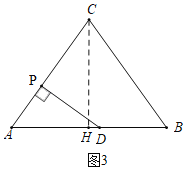
��CA��CB��CH��AB��
��AH��HB��6��
��CH��![]() ��
��![]() ��8��
��8��
��DB��DPʱ����BD��PD��x����AD��12��x��
��tanA��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��x��![]() ��
��
��AD��AB��BD��![]() ��
��
�۲�ͼ�ο�֪��6��a��![]() ʱ���������β�ͬ���۵���ʹ��B����AC����������ͬ��λ�ã�
ʱ���������β�ͬ���۵���ʹ��B����AC����������ͬ��λ�ã�

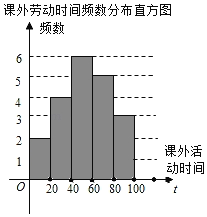
����Ŀ�������и�У�������뿪չ�Ͷ�������ijУΪ�˽����꼶ѧ��һѧ�ڲμӿ����Ͷ�ʱ�䣨��λ��h����������Ӹ�У���꼶�������˲���ѧ�������ʾ����飬�������������Ƴ����²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
�����Ͷ�ʱ��Ƶ���ֲ���
�Ͷ�ʱ����� | Ƶ�� | Ƶ�� |
��0��t��20 | 2 | 0.1 |
��20��t��40 | 4 | m |
��40��t��60 | 6 | 0.3 |
��60��t��80 | a | 0.25 |
��80��t��100 | 3 | 0.15 |
����������⣺
��1��Ƶ���ֲ�����a���� ����m���� ������Ƶ���ֲ�ֱ��ͼ����������
��2�������꼶����ѧ��400�ˣ��Թ��Ƹ�У���꼶ѧ��һѧ�ڿ����Ͷ�ʱ�䲻����60h��������
��3����֪�����Ͷ�ʱ����60h��t��80h����������Ϊ2�ˣ�����ΪŮ�����ִӸ�������ѡ2�˴���ѧУ�μӡ�ȫ����ѧ���Ͷ����顱�ݽ�������������״ͼ���б�������ѡѧ��Ϊ1��1Ů�ĸ��ʣ�
����Ŀ������ʵ������������x��x��0����y��y��0����һ���Ӧֵ���±���
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 6 | 2.9 | 2 | 1.5 | 1.2 | 1 |
��1���뻭����Ӧ������ͼ�������������ʽ��
��2����A��x1��y1����B��x2��y2���ڴ˺���ͼ���ϣ���x1��x2����y1��y2�������Ĵ�С��ϵ����˵�����ɣ�
����Ŀ��ij���ھ��꼶�����Ͻ�ѧ��������Ϊ�˽�ѧ�����������������˲���ѧ������������⣮���ݼ�������Ƴ����治������ͳ��ͼ����
��������ѧ���������Ƶ����
��� | ������ | Ƶ�� |
A | 5.1��x��5.3 | 25 |
B | 4.8��x��5.0 | 115 |
C | 4.4��x��4.7 | m |
D | 4.0��x��4.3 | 52 |
��1�������C��Ƶ��m��ֵ��
��2�������A��Բ�ĽǶ�����
��3���������ֵ4.8����������������������������Ƹ���25000�����꼶ѧ���ﵽ����������������������������ͼ����Ϣ���������������ʲô���飿