Question

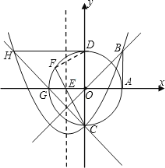
【题目】如图，过点A（1，0）作x轴的垂线与直线y＝x相交于点B，以原点O为圆心、OA为半径的圆与y轴相交于点C、D，抛物线y＝x2+px+q经过点B、C．

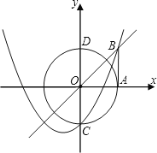
（1）求p、q的值；

（2）设抛物线的对称轴与x轴相交于点E，连接CE并延长与⊙O相交于点F，求EF的长；

（3）记⊙O与x轴负半轴的交点为G，过点D作⊙O的切线与CG的延长线相交于点H．点H是否在抛物线上？说明理由．

Answer 1

【答案】（1）p＝1，q＝﹣1；（2）；（3）点H在抛物线y＝x2+x﹣1上．详见解析

【解析】

（1）根据点A（1，0）作x轴的垂线与直线y＝x相交于点B，从而求出B点的坐标，以及C点的坐标，将B，C分别代入即可求出p，q的值；

（2）运用配方法求出二次函数的顶点坐标，再利用勾股定理求出CE的长，由Rt△CFD∽Rt△COE，求出EF的长；

（3）首先求出直线CG为：y＝x1，进而求出点H的坐标为（2，1）．代入解析式即可．

（1）∵点A（1，0）作x轴的垂线与直线y＝x相交于点B点，

∴B（1，1），

∵以原点O为圆心、OA为半径的圆与y轴相交于点C、点A（1，0），

∴C（0，﹣1）．

代入y＝x2+px+q，得，解得

故p＝1，q＝﹣1．

∴

（2）∵，

∴E（，0）

∴．

连接DF，

∵CD是直径，

∴∠CFD=90°，

又∠COE=90°，∠FCD=∠OCE

∴Rt△CFD∽Rt△COE，

得，即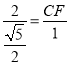

∴．

∴．

（3）设过点C、G的直线为y＝kx+b．

将点C（0，﹣1），G（﹣1，0）代入得，

解得

得直线CG为：y＝﹣x﹣1．

设过点D作⊙O的切线与CG的延长线相交于点H．

∵DH平行于x轴，

∴点H的纵坐标为1．

将y＝1代入y＝﹣x﹣1，得x＝﹣2．

∴点H的坐标为（﹣2，1）．

又当x＝﹣2时，y＝x2+x﹣1＝1，

∴点H在抛物线y＝x2+x﹣1上．