题目内容
【题目】如图,P是正三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P'AB.给出下列四个结论:①PP'=6,②AP2+BP2=CP2,③∠APB=150°;④S△ABC=36+25![]() .正确结论个数为( )
.正确结论个数为( )

A.1B.2C.3D.4
【答案】D
【解析】
由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′,由勾股定理逆定理可求△PP'B是直角三角形,AP2+BP2=CP2,可得∠P'PB=90°,可得∠APB=150°,过点A作AD垂直BP于点D,算出AD、PD,再用勾股定理算出AB,然后用公式直接求出面积.
解:连接PP′,过点A作AD⊥BP于点D,如图,
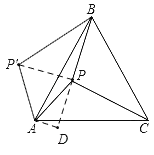
由旋转性质可知,△APC≌△AP'B,
∴AP=AP',P'B=PC=10,
∵∠P'AP=60°,
∴△APP'是等边三角形,
∴PP'=AP=6,故①正确;
∵PB=8,
∴P'B2=PB2+P'P2,
∴△PP'B是直角三角形,AP2+BP2=CP2,故②正确
∴∠P'PB=90°,
∵∠P'PA=60°,
∴∠APB=150°,故③正确;
∴∠APD=30°,
∴AD=![]() AP=3,PD=3
AP=3,PD=3![]() ,
,
∴BD=8+3![]() ,
,
在Rt△ABD中,AB2=AD2+BD2=100+48![]() ,
,
∴S△ABC=![]() AB2=36+25
AB2=36+25![]() ,故④正确.
,故④正确.
故选:D.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目