题目内容
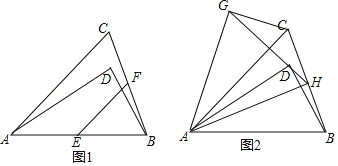
【题目】(12分)如图,矩形ABCD,AB=6cm,AD=2cm,点P以2cm/s的速度从顶点A出发沿折线A-B-C向点C运动,同时点Q以lcm/s的速度从顶点C出发向点D运动,当其中一个动点到达末端停止运动时,另一点也停止运动.
 (1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的
(1)问两动点运动几秒,使四边形PBCQ的面积是矩形ABCD面积的![]() ;
;
(2)问两动点经过多长时间使得点P与点Q之间的距离为![]() ?若存在,
?若存在,
求出运动所需的时间;若不存在,请说明理由.
【答案】
【解析】
(1).设两动点运动t秒,使四边形PBCQ的面积是矩形ABCD面积的![]()
CQ=t;PB=AB-AP=6-2t
Spbcq=1/2(CQ+PB)BC=1/2(t+6-2t)*2=6-t=4/9*6*2=16/3
t=6-16/3=2/3(秒)
(2).![]()
![]()
6-3t=-1或1
t=5/3(秒)或7/3(秒)
答:(1)两动点运动2/3秒,使四边形PBCQ的面积是矩形ABCD面积的![]() ;
;
(2)两动点经过5/3秒或7/3秒,使得点P与点Q之间的距离为![]()

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
【题目】某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和
频数分布直方图:
次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
频数 | a | 4 | 12 | 16 | 8 | 3 |

结合图表完成下列问题:
(1)a= ;
(2)补全频数分布直方图.
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀的学生人数占全班总人数的百分之几?