题目内容
已知,二次函数y=-| 1 |
| 2 |
(1)求二次函数的解析式;
(2)在x轴上,点A的左侧,求一点E,使△ECO与△CAO相似,并说明直线EC经过(1)中二次函数图象的顶点D;
(3)过(2)中的点E的直线y=
| 1 |
| 4 |
分析:(1)由二次函数y=-
x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,根据根与系数的关系与OB=2OA,即可求得m的值,则可得二次函数的解析式;
(2)由二次函数的解析式为:y=-
x2+x+4,求得A,B,C的坐标,设点E(x,0),则OE=-x,根据相似三角形的判定方法即可求得点E的坐标,然后设直线EC解析式为:y=k′x+b′,由待定系数法即可求得直线EC的解析式,又由抛物线顶点D(1,
),分别将点D的坐标代入解析式的左右式,即可得直线EC经过(1)中抛物线的顶点D;
(3)由直线y=
x+2与(1)中的二次函数y=-
x2+x+4相交于M、N两点,设M(xm,ym),N(xn,yn),可得MM′=ym,NN′=yn.又由ym,yn是方程8y2-35y+36=0的两个实数根,求得ym+yn的值,继而求得点P(t,
t+2),点Q(t,-
t2+t+4).又由S△QMN=S△QMP+S△QNP与S梯形MM'N'N:S△QMN=35:12,则可求得当t=-
或t=2时,S梯形MM'N'N:S△QMN=35:12.
| 1 |
| 2 |
(2)由二次函数的解析式为:y=-
| 1 |
| 2 |
| 9 |
| 2 |
(3)由直线y=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵二次函数y=-
x2-(m+3)x+m2-12的图象与x轴相交于A(x1,0)、B(x2,0)两点,
∴x1+x2=-2(m+3),x1x2=-2(m2-12).
又∵x1<0,x2>0,OB=2OA,
∴x2=-2x1.(3分)
整理得:m2+8m+16=0,(1分)
解得m1=m2=-4.
∴二次函数的解析式为:y=-
x2+x+4.(1分)
(2)∵二次函数的解析式为:y=-
x2+x+4,
∴点A(-2,0)、B(4,0)、C(0,4).
设点E(x,0),则OE=-x.
∵∠COA=∠EOC=90°,
要使△ECO∽△CAO,
只有
=
.
∴
=
,
∴x=-8.
∴当点E坐标为(-8,0),△ECO与△CAO相似.(1分)
设直线EC解析式为:y=k′x+b′,
将点E、点C的坐标代入得:
,
解得
,
∴直线EC的解析式为:y=
x+4.(2分)
∵抛物线顶点D(1,
),(2分)
分别将点D的坐标代入解析式的左右式,得到左式=右式.
∴直线EC经过(1)中抛物线的顶点D.(1分)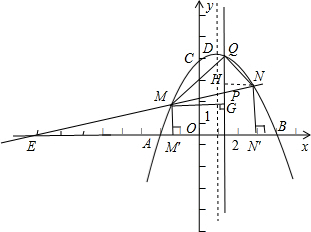
(3)存在t值,使S梯形MM'N'N:S△QMN=35:12.(1分)
∵直线y=
x+b过点E(-8,0),
∴0=
×(-8)+b,
∴b=2.
∴y=
x+2.
∴x=4(y-2)
∵直线y=
x+2与(1)中的二次函数y=-
x2+x+4相交于M、N两点,
∴y=-
×[4(y-2)]2+4(y-2)+4,整理得8y2-35y+36=0.
设M(xm,ym),N(xn,yn),
∴MM′=ym,NN′=yn.
∴ym,yn是方程8y2-35y+36=0的两个实数根,
∴ym+yn=
.
∴S梯形MM'N'N=
(ym+yn)(xn-xm).(1分)∵点P在直线y=
x+2上,点Q在(1)中的抛物线上,
∴点P(t,
t+2),点Q(t,-
t2+t+4).
∴PQ=-
t2+t+4-
t-2=-
t2+
t+2,
分别过M、N作直线PQ的垂线,垂足为点G、H,
则GM=t-xm,NH=xn-t.
∴S△QMN=S△QMP+S△QNP=
PQ(xn-xm)=
PQ•(xn-xm)=
(-
t2+
t+2)(xn-xm).(1分)
∵S梯形MM'N'N:S△QMN=35:12,
∴
=
,
∴
=
(-
t2+
t+2).
整理得:2t2-3t-2=0,
解得:t1=-
,t2=2.
∴当t=-
或t=2时,S梯形MM'N'N:S△QMN=35:12.(1分)
| 1 |
| 2 |
∴x1+x2=-2(m+3),x1x2=-2(m2-12).
又∵x1<0,x2>0,OB=2OA,
∴x2=-2x1.(3分)
整理得:m2+8m+16=0,(1分)
解得m1=m2=-4.
∴二次函数的解析式为:y=-
| 1 |
| 2 |
(2)∵二次函数的解析式为:y=-
| 1 |
| 2 |
∴点A(-2,0)、B(4,0)、C(0,4).
设点E(x,0),则OE=-x.
∵∠COA=∠EOC=90°,
要使△ECO∽△CAO,
只有
| OC |
| OE |
| OA |
| OC |
∴
| 4 |
| -x |
| 2 |
| 4 |
∴x=-8.
∴当点E坐标为(-8,0),△ECO与△CAO相似.(1分)
设直线EC解析式为:y=k′x+b′,
将点E、点C的坐标代入得:
|
解得
|
∴直线EC的解析式为:y=
| 1 |
| 2 |
∵抛物线顶点D(1,
| 9 |
| 2 |
分别将点D的坐标代入解析式的左右式,得到左式=右式.
∴直线EC经过(1)中抛物线的顶点D.(1分)

(3)存在t值,使S梯形MM'N'N:S△QMN=35:12.(1分)
∵直线y=
| 1 |
| 4 |
∴0=
| 1 |
| 4 |
∴b=2.
∴y=
| 1 |
| 4 |
∴x=4(y-2)
∵直线y=
| 1 |
| 4 |
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
设M(xm,ym),N(xn,yn),
∴MM′=ym,NN′=yn.
∴ym,yn是方程8y2-35y+36=0的两个实数根,
∴ym+yn=
| 35 |
| 8 |
∴S梯形MM'N'N=
| 1 |
| 2 |
| 1 |
| 4 |
∴点P(t,
| 1 |
| 4 |
| 1 |
| 2 |
∴PQ=-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
分别过M、N作直线PQ的垂线,垂足为点G、H,
则GM=t-xm,NH=xn-t.
∴S△QMN=S△QMP+S△QNP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∵S梯形MM'N'N:S△QMN=35:12,
∴
| ||||||
|
| 35 |
| 12 |
∴
| 35 |
| 8 |
| 35 |
| 12 |
| 1 |
| 2 |
| 3 |
| 4 |
整理得:2t2-3t-2=0,
解得:t1=-
| 1 |
| 2 |
∴当t=-
| 1 |
| 2 |
点评:此题考查了待定系数法求函数的解析式,根与系数的关系点与函数的关系以及三角形的面积问题等知识.此题综合性很强,难度很大,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 已知:二次函数的表达式为y=2x2+4x-1.
已知:二次函数的表达式为y=2x2+4x-1.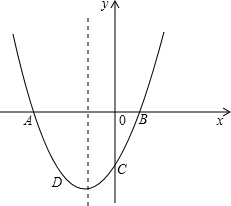 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.