题目内容
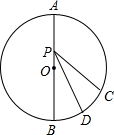 如图AB是⊙O的直径,弧BC度数是60,D是劣弧BC的中点,P是AB上的动点,若⊙O的半径为1,则PC+PD的最小值是
如图AB是⊙O的直径,弧BC度数是60,D是劣弧BC的中点,P是AB上的动点,若⊙O的半径为1,则PC+PD的最小值是| 2 |
| 2 |
分析:作D点关于AB的对称点E,连CE交AB于P点,连EC,根据两点之间线段最短得到CE是PD+PC的最小值.在△OCE中,利用勾股定理即可求解.
解答: 解:作D点关于AB的对称点E,连CE交AB于P点,
解:作D点关于AB的对称点E,连CE交AB于P点,
∵弧BC度数是60,D是劣弧BC的中点,
∴弧DC=弧BD=弧BE=30°
∴∠CDE=90°
∴CE是PD+PC的最小值.
又∵OC=OE,
∴△COE为等腰直角三角形.
∵OE=OC=1,
∴CE=
.
∴PD+PC的最小值为
.
故答案是:
.
 解:作D点关于AB的对称点E,连CE交AB于P点,
解:作D点关于AB的对称点E,连CE交AB于P点,∵弧BC度数是60,D是劣弧BC的中点,
∴弧DC=弧BD=弧BE=30°
∴∠CDE=90°
∴CE是PD+PC的最小值.
又∵OC=OE,
∴△COE为等腰直角三角形.
∵OE=OC=1,
∴CE=
| 2 |
∴PD+PC的最小值为
| 2 |
故答案是:
| 2 |
点评:本题考查了圆周角定理,正确确定P点的位置是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
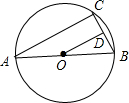 如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
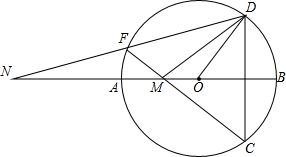 CF交AB于点M,连接DF并延长交BA的延长线于点N.
CF交AB于点M,连接DF并延长交BA的延长线于点N.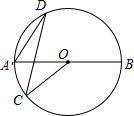 如图AB是⊙O的直径,∠D=35°,则∠AOC=
如图AB是⊙O的直径,∠D=35°,则∠AOC=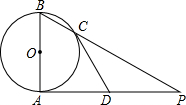 (2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C. (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.