题目内容
如图AB是⊙O的直径,弦DC⊥AB于点E,在 | AD |
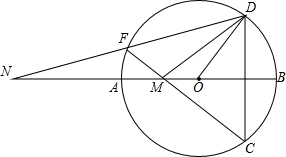 CF交AB于点M,连接DF并延长交BA的延长线于点N.
CF交AB于点M,连接DF并延长交BA的延长线于点N.求证:
(1)∠DFC=∠DOB;
(2)MN•OM=MC•FM.
分析:(1)连接OC,由圆周角定理,易知∠DFC=
∠DOC,根据垂径定理,易证∠DOB=
∠DOC,由此可证得∠DFC=∠DOB;
(2)可通过证△NFM∽△MOC来得出所求的结论.
| 1 |
| 2 |
| 1 |
| 2 |
(2)可通过证△NFM∽△MOC来得出所求的结论.
解答: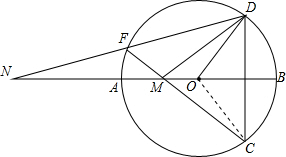 证明:(1)连接OC,
证明:(1)连接OC,
∵DC⊥AB,OD=OC,
∴∠DOB=
∠DOC.
∵∠DFC=
∠DOC,
∴∠DFC=∠DOB.
(2)∵∠DFC=∠DOB,
∴∠DFC=∠BOC.
∴∠MFN=∠MOC.
又∵∠FMA=∠OMC,
∴△NFM∽△MOC.
∴
=
,即MN•OM=MC•FM.
 证明:(1)连接OC,
证明:(1)连接OC,∵DC⊥AB,OD=OC,
∴∠DOB=
| 1 |
| 2 |
∵∠DFC=
| 1 |
| 2 |
∴∠DFC=∠DOB.
(2)∵∠DFC=∠DOB,
∴∠DFC=∠BOC.
∴∠MFN=∠MOC.
又∵∠FMA=∠OMC,
∴△NFM∽△MOC.
∴
| MN |
| FM |
| MC |
| OM |
点评:本题主要考查圆周角定理和相似三角形的判定和性质;证线段积的关系,通常是证这些线段所在的三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
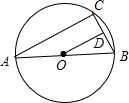 如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长. 如图AB是⊙O的直径,∠D=35°,则∠AOC=
如图AB是⊙O的直径,∠D=35°,则∠AOC= (2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C. (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.