题目内容
【题目】在平面直角坐标系中,点A、B的坐标分别为(﹣3,0)、(3,0),点P在反比例函数y= ![]() 的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
的图象上.若△PAB为直角三角形,则满足条件的点P的个数为( )
A. 2个 B. 4个 C. 5个 D. 6个
【答案】A
【解析】
设点P的坐标为(x,y),分∠APB=90°、∠PAB=90°和∠PBA=90°三种情况考虑:当∠APB=90°时,以AB为直径作圆,由圆与双曲线无交点可知此时点P不存在;当∠PAB=90°时,可找出x=-3,进而可得出点P的坐标;当∠PBA=90°时,可找出x=3,进而可得出点P的坐标.综上即可得出结论.
设点P的坐标为(x,y),
当∠APB=90°时,以AB为直径作圆,如图所示,
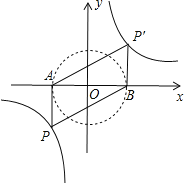
∵圆与双曲线无交点,
∴点P不存在;
当∠PAB=90°时,x=-3,
y=![]() =-3,
=-3,
∴点P的坐标(-3,-3),
当∠PBA=90°时,x=3,
y=![]() =3,
=3,
∴点P的坐标为(3,3).
综上所述:满足条件的点P有2个.
故选:A.

练习册系列答案
相关题目