题目内容
【题目】一枚正方形骰子的六个面上分别标有1～6六个正整数，连续投掷这枚骰子两次，朝上的两个数依次作为一个点的横坐标、纵坐标，则这个点落在双曲线
上的概率为（ ）.
A. 
B. 
C. 
D. 
【答案】C
【解析】
首先根据题意列出表格，然后由表格即可求得所有等可能的结果与这个点落在双曲线
上的情况，再利用概率公式即可求得答案．
列表得：
6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
5 | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
4 | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
3 | （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
2 | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
1 | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
1 | 2 | 3 | 4 | 5 | 6 |
∵共有36种等可能的结果，落在双曲线上的有（2，6），（3，4），（4，3），（6，2）共4种情况，
∴这个点落在双曲线上的概率为：
．
故选C．
孟建平名校考卷系列答案
【题目】星马公司到某大学从应届毕业生中招聘公司职员，对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试成果认定，三项得分满分都为100分，三项的分数分别为 
的比例计入每人的最后总分，有4位应聘者的得分如下所示：
项目 得分 应聘者 | 专业知识 | 英语水平 | 参加社会实践与社团活动等 |
A | 85 | 85 | 90 |
B | 85 | 85 | 70 |
C | 80 | 90 | 70 |
D | 80 | 90 | 50 |
（1）写出4位应聘者的总分；
（2）已知这4人专业知识、英语水平、参加社会实践与社团活动等三项的得分对应的方差分别为12.5、6.25、200，你对应聘者有何建议？
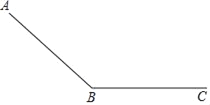
【题目】如图，一个滑道由滑坡（AB段）和缓冲带（BC段）组成，滑雪者在滑坡上滑行的距离y1（单位：m）和滑行时间t1（单位s）满足二次函数关系，并测得相关数据：
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2（单位：m）和滑行时间t2（单位：s）满足：y2=52t2﹣2t22，滑雪者从A出发在缓冲带BC上停止，一共用了23s．
（1）求y1和t1满足的二次函数解析式；
（2）求滑坡AB的长度．
