题目内容
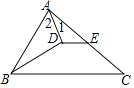
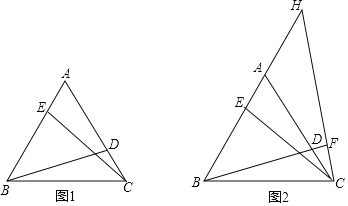
【题目】(1)如图1,点![]() 、
、![]() 分别是等边
分别是等边![]() 边
边![]() 、
、![]() 上的点,连接
上的点,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
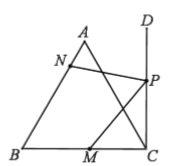
(2)如图2,在(1)问的条件下,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() 交
交![]() 延长线于点
延长线于点![]() ,.若
,.若![]() ,求证:
,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)根据等边三角形的性质可得AC=CB,∠ABC=∠A=∠ACB=60°,然后利用SAS即可证出△AEC≌△CDB,从而得出BD=CE;
(2)根据全等三角形的性质可得∠CBD=∠ACE,从而证出∠ABD=∠ECB,然后根据等边对等角可得∠BFC=∠BCF,从而证出∠H=∠ECH,最后根据等角对等边即可证出结论.
证明:(1)∵△ABC为等边三角形
∴AC=CB,∠ABC=∠A=∠ACB=60°
在△AEC和△CDB中
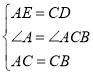
∴△AEC≌△CDB(SAS)
∴BD=CE
(2)∵△AEC≌△CDB
∴∠CBD=∠ACE
∴∠ABC-∠CBD=∠ACB-∠ACE
∴∠ABD=∠ECB
又∵BF=BC,
∴∠BFC=∠BCF
∵∠ABD+∠H=∠BFC,∠ECB+∠ECH=∠BCF
∴∠H=∠ECH,
∴EH=EC

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目