题目内容
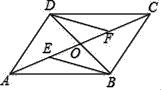
【题目】如图所示,四边形ABCD的对角线AC、BD交于点O,若OE=OF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)求证:四边形DEBF是平行四边形;
(3)若OD=OE=OF,则四边形DEBF是什么特殊的四边形,请证明.
【答案】见解析
【解析】整体分析:
(1)用ASA证明△BOE≌△DOF;(2)连接DE、BF,用对角线互相平分的四边形是平行四边形证明;(3)四边形DEBF是平行四边形,且对角线相等.
(1)证明:∵DF∥BE,
∴∠DFE=∠BEO,
在△BOE和△DOF中,
∠DFE=∠BEO,OF=OE,∠DOF=∠EOB,
∴△BOE≌△DOF.
(2)证明:连接DE、BF.
∵△BOE≌△DOF,
∴OD=OB,∵OE=OF,
∴四边形DEBF是平行四边形.

(3)若OD=OE=OF,则四边形DEBF是矩形.
理由:∵OD=OE=OF=OB,
∴BD=EF,
∵四边形DEBF是平行四边形,
∴四边形DEBF是矩形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某商店需要购进A.B两种商品共160件,其进价和售价如表:
A | B | |
进价(元/件) | 15 | 35 |
售价(元/件) | 20 | 45 |
(1)当A.B两种商品分别购进多少件时,商店计划售完这批商品后能获利1100元;
(2)若商店计划购进A种商品不少于66件,且销售完这批商品后获利多于1260元,请你帮该商店老板预算有几种购货方案?获利最大是多少元?