Question

如图，在矩形ABCD中，E为AD的中点，EF⊥EC交AB于F，连结FC
（AB＞AE）

【小题1】△AEF与△EFC是否相似？若相似，证明你的结论；若不相似，请说明理由；
【小题2】设＝k，是否存在这样的k值，使得△AEF∽△BFC，若存在，证明你的结论并求出k的值；若不存在，说明理由

Answer 1

【小题1】如图，是相似．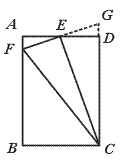

延长FE，与CD的延长线交于点G．
在Rt△AEF与Rt△DEG中，
∵　E是AD的中点，
∴　AE＝ED．
∵　∠AEF＝∠DEG，
∴　△AFE≌△DGE．
∴　∠AFE＝∠DGE．
∴　E为FG的中点．
又　CE⊥FG，
∴　FC＝GC．
∴　∠CFE＝∠G．
∴　∠AFE＝∠EFC．
又　△AEF与△EFC均为直角三角形，
∴　△AEF∽△EFC．
【小题2】存在．如果∠BCF＝∠AEF，即k＝＝时，△AEF∽△BCF．
证明：当＝时，＝，
∴　∠ECG＝30°．
∴　∠ECG＝∠ECF＝∠AEF＝30°．
∴　∠BCF＝90°－60°＝30°．
又　△AEF和△BCF均为直角三角形，
∴　△AEF∽△BCF．
因为EF不平行于BC，
∴　∠BCF≠∠AFE．
∴　不存在第二种相似情况

解析