题目内容
【题目】如图,梯形ABCD中,AD∥BC,BC=20cm,AD=10cm,现有两个动点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,线段PQ与BD相交于点E,过E作EF∥BC交CD于点F,射线QF交BC的延长线于点H,设动点P、Q移动的时间为t(单位:秒,0<t<10). 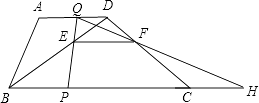
(1)当t为何值时,四边形PCDQ为平行四边形?
(2)在P、Q移动的过程中,线段PH的长是否发生改变?如果不变,求出线段PH的长;如果改变,请说明理由.
【答案】
(1)解:∵AD∥BC,BC=20cm,AD=10cm,点P、Q分别从B、D两点同时出发,点P以每秒2cm的速度沿BC向终点C移动,点Q以每秒1cm的速度沿DA向终点A移动,
∴DQ=t,PC=20﹣2t,
∵若四边形PCDQ为平行四边形,则DQ=PC,
∴20﹣2t=t,
解得:t= ![]()
(2)解:线段PH的长不变,
∵AD∥BH,P、Q两点的速度比为2:1,
∴△QED∽△PEB,QD:BP=1:2,
∴QE:EP=ED:BE=1:2,
∵EF∥BH,
∴ED:DB=EF:BC=1:3,
∵BC=20,
∴EF= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PH=20cm
【解析】(1)如果四边形PCDQ为平行四边形,则DQ=CP,根据P、Q两点的运动速度,结合运动时间t,求出DQ、CP的长度表达式,解方程即可;(2)PH的长度不变,根据P、Q两点的速度比,即可推出QD:BP=1:2,根据平行线的性质推出三角形相似,得出相似比,即可推出PH=20.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握梯形的定义(一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为285元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六.星期日休市)
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化(与前一天收盘价比较) | +7 | +5 |
|
| +8 |
问:(1)本周星期三黄金的收盘价是多少?
(2)本周黄金收盘时的最高价.最低价分别是多少?
(3)上周,小王以周五的收盘价285元/克买入黄金1000克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金1000克,他的收益情况如何?