题目内容
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.

(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积.(结果保留π)

(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积.(结果保留π)
(1)BC所在直线与小圆相切,理由见试题解析;(2)BC=AD+AC,理由见试题解析;(3)16 cm2.
cm2.
 cm2.
cm2.试题分析:(1)只要证明OE垂直BC即可得出BC是小圆的切线,即与小圆的关系是相切;
(2)利用全等三角形的判定得出Rt△OAD≌Rt△OEB,从而得出EB=AD,从而得到三者的关系是前两者的和等于第三者;
(3)根据大圆的面积减去小圆的面积即可得到圆环的面积.
试题解析:(1)BC所在直线与小圆相切.
理由如下:过圆心O作OE⊥BC,垂足为E;∵AC是小圆的切线,AB经过圆心O,∴OA⊥AC;又∵CO平分∠ACB,OE⊥BC,∴OE=OA,∴BC所在直线是小圆的切线;
(2)AC+AD=BC.理由如下:
连接OD.∵AC切小圆O于点A,BC切小圆O于点E,∴CE=CA;∵在Rt△OAD与Rt△OEB中,
 ,∴Rt△OAD≌Rt△OEB(HL),∴EB=AD;∵BC=CE+EB,∴BC=AC+AD;
,∴Rt△OAD≌Rt△OEB(HL),∴EB=AD;∵BC=CE+EB,∴BC=AC+AD;(3)∵∠BAC=90°,AB=8cm,BC=10cm,∴AC=6cm;∵BC=AC+AD,∴AD=BC﹣AC=4cm,∵圆环的面积为:S=π(OD)2﹣π(OA)2=π(OD2﹣OA2),又∵OD2﹣OA2=AD2,∴S=42π=16π(cm2).


练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
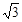 )为圆心,作⊙M交x轴于A、B两点,交y轴于C、D两点,连结AM并延长交⊙M于点P,连结PC交x轴于点E,连结DB,∠BDC=30°.
)为圆心,作⊙M交x轴于A、B两点,交y轴于C、D两点,连结AM并延长交⊙M于点P,连结PC交x轴于点E,连结DB,∠BDC=30°.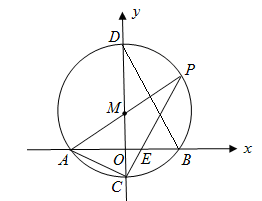

 ,求PO的长.
,求PO的长.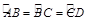 ,BA和CD的延长线相交于P,∠P=40°,则∠ACD的度数是( )
,BA和CD的延长线相交于P,∠P=40°,则∠ACD的度数是( )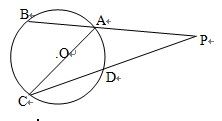



 cm长为半径画圆则 A、B、M三点在圆外的是 .在圆上的是 。
cm长为半径画圆则 A、B、M三点在圆外的是 .在圆上的是 。