题目内容
【题目】已知点A(a,0)、B(b,0),且(a+4)2+|b﹣2|=0. 
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的 ![]() ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】
(1)解:∵(a+4)2+|b﹣2|=0,
∴a+4=0,b﹣2=0,
∴a=﹣4,b=2
(2)解:如图1,

∵A(﹣4,0)、B(2,0),
∴AB=6,
∵三角形ABC的面积是15,
∴ ![]() ABOC=15,
ABOC=15,
∴OC=5,
∴C(0,5)
(3)解:存在,如图2,
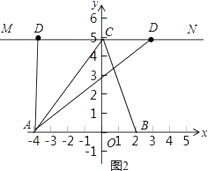
∵三角形ABC的面积是15,
∴S△ACD= ![]() CDOC=
CDOC= ![]() 15,
15,
∴ ![]() CD×5=
CD×5= ![]() 15,
15,
∴CD=3,
∴D(3.5)或(﹣3,5).
【解析】(1)根据非负数的性质列方程即可得到结论;(2)由A(﹣4,0)、B(2,0),得到AB=6,根据三角形ABC的面积是15列方程即可得到即可;(3)根据三角形ABC的面积是15列方程即可得到结论.
【考点精析】解答此题的关键在于理解绝对值的相关知识,掌握正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离,以及对三角形的面积的理解,了解三角形的面积=1/2×底×高.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】肇庆市某一周的PM2.5(大气中直径小于等于2.5微米的颗粒物,也称可入肺颗粒物)指数如下表:
PM2.5指数 | 150 | 155 | 160 | 165 |
天 数 | 3 | 2 | 1 | 1 |
则该周PM2.5指数的众数和中位数分别是( )
A. 150,150B. 150,155C. 155,150D. 150,152.5