Question

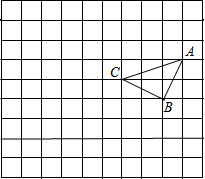
如图，在Rt△ABC中，∠ABC=90°，AC=20，AB=10

3

，将BC向BA方向翻折过去，使点C落在BA上的点C′，折痕为BE，则EC的长度是（　　）

A．10 3

B．10 3 -10

C．20-10 3

D．10+2 3

Answer 1

作ED⊥BC于D，由折叠的性质可知∠DBE=∠ABE=45°，
∵∠ABC=90°，AC=20，AB=10

3

，
∴sin∠C=

10 3

20

=

3

2

，
∴∠C=60°，
设所求的EC为x，则CD=

1

2

x，BD=ED=

3

2

x，
∵∠ABC=90°，AC=20，AB=10

3

，
∴BC=

202-(10 3 )2

=10，
∵CD+BD=10，
∴

1

2

x+

3

2

x=10，
解得：x=10

3

-10，
∴CE=10

3

-10，
故选：B．