题目内容
如图,已知抛物线与x轴交于A(-1,0)、E(3,0)两点,与y轴交于点B(0,3)。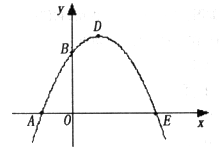
(1)求抛物线的解析式;
(2)设抛物线顶点为D,求四边形AEDB的面积;
(3)△AOB与△DBE是否相似?如果相似,请给以证明;如果不相似,请说明理由。
(1)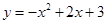 ;(2)9;(3)△AOB∽△DBE.理由见解析.
;(2)9;(3)△AOB∽△DBE.理由见解析.
解析试题分析:(1)已知了抛物线图象上的三点坐标,可用待定系数法求出抛物线的解析式;
(2)根据抛物线的解析式,易求得抛物线顶点D的坐标;过D作DF⊥x轴于F,那么四边形AEDB的面积就可以由△AOB、△DEF、梯形BOFD的面积和求得.
(3)先判定△DBE是直角三角形,即可得证△AOB∽△DBE.
试题解析:(1)∵抛物线与y轴交于点(0,3),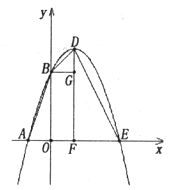
∴设抛物线解析式为
根据题意,得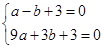 ,
,
解得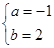
∴抛物线的解析式为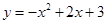 ;
;
(2)由顶点坐标公式求得顶点坐标为(1,4)
设对称轴与x轴的交点为F
∴四边形ABDE的面积=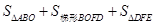
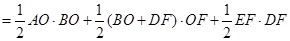
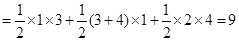 ;
;
(3)相似
如图,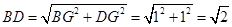 ;
;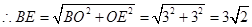
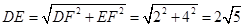
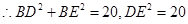
即: ,所以△BDE是直角三角形
,所以△BDE是直角三角形
∴∠AOB=∠DBE=90°,且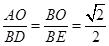 ,
,
∴△AOB∽△DBE.
考点: 二次函数综合题.

练习册系列答案
相关题目
近期,海峡两岸关系的气氛大为改善.大陆相关部门对原产台湾地区的15种水果实施进口零关税措施,扩大了台湾水果在大陆的销售.某经销商销售了台湾水果凤梨,根据以往销售经验,每天的售价与销售量之间有如下关系:
| 每千克售价(元) | 40 | 39 | 38 | 37 | … | 30 |
| 每天销量(千克) | 60 | 65 | 70 | 75 | … | 110 |
(1)写出y与x间的函数关系式;
(2)如果凤梨的进价是20元/千克,若不考虑其他情况,那么单价从40元/千克下调多少元时,当天的销售利润W最大?利润最大是多少?
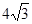 时,求x的值.
时,求x的值.

 轴上方的抛物线上是否存在一点M,过M作MG
轴上方的抛物线上是否存在一点M,过M作MG
 PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
PCA相似.若存在,请求出M点的坐标;否则,请说明理由. 的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,―3)点,点P是直线BC下方的抛物线上一动点。
的图象与x轴交于A、B两点,A点在原点的左则,B点的坐标为(3,0),与y轴交于C(0,―3)点,点P是直线BC下方的抛物线上一动点。
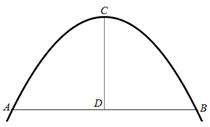
 的图像经过点(4,1)和(
的图像经过点(4,1)和( ,6).
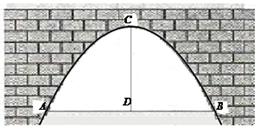
,6). 轴建立直角坐标系,桥洞上沿形状恰好是抛物线
轴建立直角坐标系,桥洞上沿形状恰好是抛物线 的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
的图像.桥洞两侧壁上各有一盏距离水面4米高的景观灯.请求出这两盏景观灯间的水平距离.
