题目内容
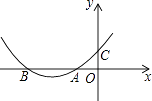
【题目】已知x轴上有点A（1，0），点B在y轴上，点C（m，0）为x轴上一动点且m＜﹣1，连接AB，BC，tan∠ABO= 
，以线段BC为直径作⊙M交直线AB于点D，过点B作直线l∥AC，过A，B，C三点的抛物线为y=ax2+bx+c，直线l与抛物线和⊙M的另一个交点分别是E，F．
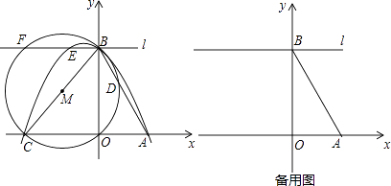
（1）求B点坐标；
（2）用含m的式子表示抛物线的对称轴；
（3）线段EF的长是否为定值？如果是，求出EF的长；如果不是，说明理由．
（4）是否存在点C（m，0），使得BD= AB？若存在，求出此时m的值；若不存在，说明理由．
【答案】
（1）
解：∵tan∠ABO= 
，且A（1，0），
∴OB=2，即：点B的坐标为（0，2）
（2）
解：点C（m，0），A（1，0），B（0，2）在抛物线y=ax2+bx+c上，
∴ 
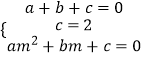
解之得：b=﹣ 
，a= 
，
∴x=﹣ 
= 
．
即：抛物线的对称轴为x=
（3）
解：∵点E在抛物线y=ax2+bx+c上，又在直线y=2上，
∴2=ax2+bx+2
∴x1=0，x2=﹣ 
∴E（﹣ ，2），
又∵直线l∥x轴，BC是⊙M的直径，
∴BF∥OC，BF=OC，
∴F（m，2）
∴EF=﹣ ﹣m，
∵点C（m，0）为x轴上一动点且m＜﹣1，
∴m的值是一个变量，
即：线段EF的长不是定值
（4）
解：如下图所示：连接CD
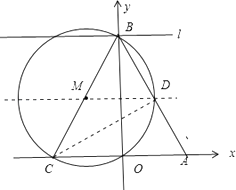
∵BCS是⊙M的直径，
∴∠CDB=90°，
∵若BD= 
AB，即BD=DA
则易证CB=CA
∴ 
=1﹣m
解之得m=﹣ 
，
即：存在一点C（﹣ ，0），使得BD= AB
【解析】（1）根据正切函数的定义及点A的坐标求解；（2）因为点C、A、B在抛物线上，故代入其坐标列方程组求解即可；（3）点E（x，y）既在抛物线y=ax2+bx+2上，又在直线y=2上，所以有2=ax2+bx+2，由此可知E（﹣ ，2），又因为直线l∥x轴，BC是⊙M的直径，由圆的对称性可知BF∥OC且BF=OC，所以F（m，2），由此可分析EF长；（4）连接CD，因为BC为圆的直径，所以∠BDC=90°，若BD= AB，可证明CA=CB，由此可求得符合题意的点C（﹣ ，0）．
