题目内容
【题目】阅读下列材料:小华遇到这样一个问题:
已知:如图1,在△ABC中,三边的长分别为AB= ![]() ,AC=
,AC= ![]() ,BC=2,求∠A的正切值.
,BC=2,求∠A的正切值.
小华是这样解决问题的:
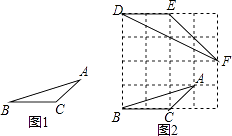
如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.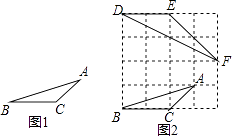
(1)如图2,△DEF中与∠A相等的角为 , ∠A的正切值为 .
(2)参考小华的方法请解决问题:若△LMN的三边分别为LM=2,MN=2 ![]() ,LN=2
,LN=2 ![]() ,求∠N的正切值.
,求∠N的正切值.
【答案】
(1)∠D;![]()
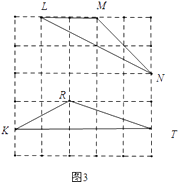
(2)解:在图3中,作一个△RKT,使得PK= ![]() ,RT=
,RT= ![]() ,KT=5,
,KT=5,
∵LM=2,NM=2 ![]() ,LN=2
,LN=2 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴△RKT∽△MLN,
∴∠T=∠N,
∴tan∠N=tan∠T= ![]() .
.
【解析】解:(1)由图2 可知DE=2,EF=2 ![]() ,DF=2
,DF=2 ![]() ,AB=
,AB= ![]() ,AC=
,AC= ![]() ,BC=2,
,BC=2,
∵ ![]() ,
,
∴△DEF∽△ACB,
∴∠D=∠A,
∴tan∠A=tan∠D= ![]() ,
,
故答案分别为∠D, ![]()

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目