Question

【题目】材料1：反射定律

当入射光线AO照射到平面镜上时，将遵循平面镜反射定律，即反射角（∠BOM）的大小等于入射角（∠AOM）的大小，显然，这两个角的余角也相等，其中法线（OM）与平面镜垂直，并且满足入射光线、反射光线（OB）与法线在同一个平面．

材料2：平行逃逸角

对于某定角∠AOB=α（0°＜α＜90°），点P为边OB上一点，从点P发出一光线PQ（射线），其角度为∠BPQ=β（0°＜β＜90°），当光线PQ接触到边OA和OB时会遵循反射定律发生反射，当光线PQ经过n次反射后与边OA或OB平行时，称角为定角α的n阶平行逃逸角，特别地，当光线PQ直接与OA平行时，称角β为定角α的零阶平行逃逸角．

（1）已知∠AOB=α=20°，

①如图1，若PQ∥OA，则∠BPQ=　 　°，即该角为α的零阶平行逃逸角；

②如图2，经过一次反射后的光线P1Q∥OB，此时的∠BPP1为α的平行逃逸角，求∠BPP1的大小；

③若经过两次反射后的光线与OA平行，请补全图形，并直接写出α的二阶平行逃逸角为　 　°；

（2）根据（1）的结论，归纳猜想对于任意角α（0°＜α＜90°），其n（n为自然数）阶平行逃逸角β=　 　（用含n和a的代数式表示）．

Answer 1

【答案】（1）①20；②∠BPP1=40°③60°；（2）（n+1）α．

【解析】

（1）①两直线平行，同位角相等；②由“反射定律”可得∠AP1Q=∠PP1O，再由P1Q∥OB可得∠AP1Q=∠PP1O=∠AOB=20°；③先作PQ∥AO，再根据“反射定律”先画出P2P1，再画出P1P.

（3）分别从零阶、一阶、二阶逃逸角与∠α的关系中归纳一般性关系.

解：（1）①如图①中，∵PQ∥OA，

∴∠BPQ=∠AOB=20°，

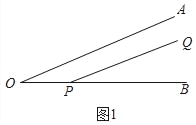
故答案为20．

②如图2中，

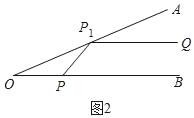
∵P1Q∥OB，

∴∠AP1Q=∠PP1O=∠AOB=20°，

∴∠BPP1=∠AOB+∠PP1O=40°．

③如图3中，如图所示，α的二阶平行逃逸角为20°×3=60°，

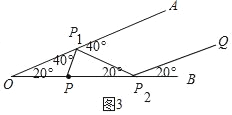
（2）由（1）可知：α的零阶平行逃逸角为α，α的1阶平行逃逸角为2α，α的二阶平行逃逸角为3α，

…，由此可以推出，α的n阶平行逃逸角为（n+1）α，

故答案为（n+1）α．