ΧβΡΩΡΎ»ί
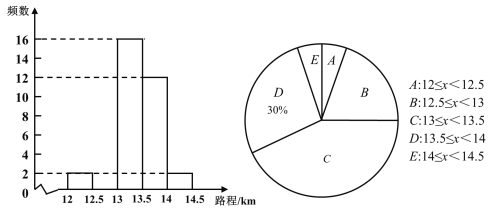
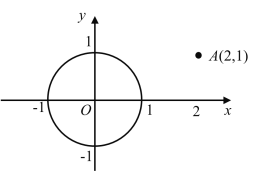
ΓΨΧβΡΩΓΩΈ“Ο«÷ΣΒάΘ§ΝΫΒψ÷°ΦδœΏΕΈΉνΕΧΘ§“ρ¥ΥΘ§Ν§Ϋ”ΝΫΒψΦδœΏΕΈΒΡ≥ΛΕ»Ϋ–ΉωΝΫΒψΦδΒΡΨύάκΘΜΆ§άμΘ§Ν§Ϋ”÷±œΏΆβ“ΜΒψ”κ÷±œΏ…œΗςΒψΒΡΥυ”–œΏΕΈ÷–Θ§¥ΙœΏΕΈΉνΕΧΘ§“ρ¥ΥΘ§÷±œΏΆβ“ΜΒψΒΫ’βΧθ÷±œΏΒΡ¥ΙœΏΕΈΒΡ≥ΛΕ»Θ§Ϋ–ΉωΒψΒΫ÷±œΏΒΡΨύάκΘ°άύΥΤΒΊΘ§Ν§Ϋ”«ζœΏΆβ“ΜΒψ”κ«ζœΏ…œΗςΒψΒΡΥυ”–œΏΕΈ÷–Θ§ΉνΕΧœΏΕΈΒΡ≥ΛΕ»Θ§Ϋ–ΉωΒψΒΫ«ζœΏΒΡΨύάκΘ°“ά¥ΥΕ®“εΘ§»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ_____Θ°
ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ_____Θ°
ΓΨ¥πΑΗΓΩ![]()
ΓΨΫβΈωΓΩ
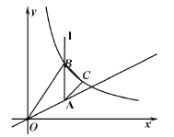
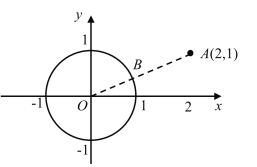
Ν§Ϋ”OAΘ§”κ‘≤OΫΜ”ΎΒψBΘ§ΗυΨίΧβΗ…÷–ΒΡΗ≈ΡνΒΟΒΫΒψΒΫ‘≤ΒΡΨύάκΦ¥ΈΣOBΘ§‘Ό«σ≥ωOAΘ§ΫαΚœ‘≤OΑκΨΕΩ…ΒΟΫαΙϊ.
ΫβΘΚΗυΨίΧβ“βΩ…ΒΟΘΚ
ΒψΒΫ‘≤ΒΡΨύάκΈΣΘΚΗΟΒψ”κ‘≤…œΗςΒψΒΡΝ§œΏ÷–Θ§ΉνΕΧΒΡœΏΕΈ≥ΛΕ»Θ§
Ν§Ϋ”OAΘ§”κ‘≤OΫΜ”ΎΒψBΘ§
Ω…÷ΣΘΚΒψAΚΆ‘≤O…œΒψB÷°ΦδΒΡΝ§œΏΉνΕΧΘ§
ΓΏAΘ®2Θ§1Θ©Θ§
ΓύOA=![]() =
=![]() Θ§
Θ§
ΓΏ‘≤OΒΡΑκΨΕΈΣ1Θ§
ΓύAB=OA-OB=![]() Θ§
Θ§
ΓύΒψ![]() ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ
ΒΫ“‘‘≠ΒψΈΣ‘≤–ΡΘ§“‘1ΈΣΑκΨΕΒΡ‘≤ΒΡΨύάκΈΣ![]() Θ§
Θ§
Ι ¥πΑΗΈΣΘΚ![]() .
.

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
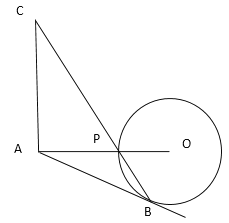
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ–Γ‘Τ‘Ύ―ßœΑΙΐ≥Χ÷–”ωΒΫ“ΜΗωΚ· ΐ![]() Θ°œ¬Οφ «–Γ‘ΤΕ‘ΤδΧΫΨΩΒΡΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
Θ°œ¬Οφ «–Γ‘ΤΕ‘ΤδΧΫΨΩΒΡΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
Θ®1Θ©Β±![]() ±Θ§Ε‘”ΎΚ· ΐ
±Θ§Ε‘”ΎΚ· ΐ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ Θ§«“
ΒΡ‘ω¥σΕχ Θ§«“![]() ΘΜΕ‘”ΎΚ· ΐ
ΘΜΕ‘”ΎΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ Θ§«“
ΒΡ‘ω¥σΕχ Θ§«“![]() ΘΜΫαΚœ…œ ωΖ÷ΈωΘ§Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§Ε‘”ΎΚ· ΐ
ΘΜΫαΚœ…œ ωΖ÷ΈωΘ§Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§Ε‘”ΎΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ Θ°
ΒΡ‘ω¥σΕχ Θ°
Θ®2Θ©Β±![]() ±Θ§Ε‘”ΎΚ· ΐ
±Θ§Ε‘”ΎΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() ”κ
”κ![]() ΒΡΦΗΉιΕ‘”Π÷Β»γœ¬±μΘΚ
ΒΡΦΗΉιΕ‘”Π÷Β»γœ¬±μΘΚ
| 0 |
| 1 |
| 2 |
| 3 |
|
| 0 |
|
|
| 1 |
|
|
|
ΉέΚœ…œ±μΘ§Ϋχ“Μ≤ΫΧΫΨΩΖΔœ÷Θ§Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχ‘ω¥σΘ°‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ
ΒΡ‘ω¥σΕχ‘ω¥σΘ°‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Μ≠≥ωΒ±
÷–Θ§Μ≠≥ωΒ±![]() ±ΒΡΚ· ΐ
±ΒΡΚ· ΐ![]() ΒΡΆΦœσΘ°
ΒΡΆΦœσΘ°
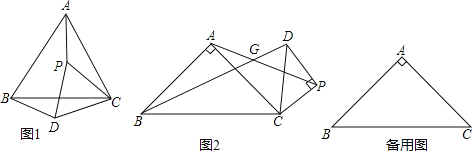
Θ®3Θ©ΙΐΒψ(0Θ§m)Θ®![]() Θ©ΉςΤΫ––”Ύ
Θ©ΉςΤΫ––”Ύ![]() ÷αΒΡ÷±œΏ
÷αΒΡ÷±œΏ![]() Θ§ΫαΚœΘ®1Θ©Θ®2Θ©ΒΡΖ÷ΈωΘ§ΫβΨωΈ ΧβΘΚ»τ÷±œΏ
Θ§ΫαΚœΘ®1Θ©Θ®2Θ©ΒΡΖ÷ΈωΘ§ΫβΨωΈ ΧβΘΚ»τ÷±œΏ![]() ”κΚ· ΐ
”κΚ· ΐ![]() ΒΡΆΦœσ”–ΝΫΗωΫΜΒψΘ§‘ρ
ΒΡΆΦœσ”–ΝΫΗωΫΜΒψΘ§‘ρ![]() ΒΡΉν¥σ÷Β « Θ°
ΒΡΉν¥σ÷Β « Θ°