题目内容
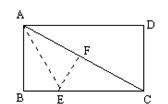
如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.

(1)试说明∠ABD=∠CBD.
(2)若∠C=2∠E,试说明AB=DC.

(1)试说明∠ABD=∠CBD.
(2)若∠C=2∠E,试说明AB=DC.
解:(1) AD∥BC
AD∥BC
 ADB=
ADB= CBD
CBD
又 AD=AB
AD=AB
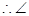 ADB=
ADB= ABD
ABD
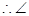 ABD=
ABD= CBD
CBD
(2)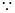 AE∥BD
AE∥BD
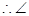 E=
E= BDC=
BDC= ABD
ABD
又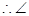 C=2
C=2 E
E
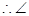 C=2
C=2 BDC=
BDC= ABC
ABC
 梯形ABCD为等腰梯形
梯形ABCD为等腰梯形
 AB=CD
AB=CD
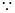 AD∥BC
AD∥BC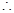
 ADB=
ADB= CBD
CBD又
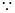 AD=AB
AD=AB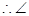 ADB=
ADB= ABD
ABD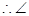 ABD=
ABD= CBD
CBD(2)
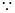 AE∥BD
AE∥BD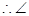 E=
E= BDC=
BDC= ABD
ABD又
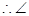 C=2
C=2 E
E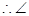 C=2
C=2 BDC=
BDC= ABC
ABC 梯形ABCD为等腰梯形
梯形ABCD为等腰梯形 AB=CD
AB=CD(1)由AD∥BC根据平行线的性质可得 ADB=
ADB= CBD,由AD=AB根据等边对等角可得
CBD,由AD=AB根据等边对等角可得 ADB=
ADB= ABD,即得
ABD,即得 ABD=
ABD= CBD;
CBD;
(2)由AE∥BD根据平行线的性质可得 E=
E= BDC=
BDC= ABD,由已知
ABD,由已知 C=2
C=2 E可得
E可得 C=
C= ABC,即得结论。
ABC,即得结论。
 ADB=
ADB= CBD,由AD=AB根据等边对等角可得
CBD,由AD=AB根据等边对等角可得 ADB=
ADB= ABD,即得
ABD,即得 ABD=
ABD= CBD;
CBD;(2)由AE∥BD根据平行线的性质可得
 E=
E= BDC=
BDC= ABD,由已知
ABD,由已知 C=2
C=2 E可得
E可得 C=
C= ABC,即得结论。
ABC,即得结论。
练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目

 ②△ACD≌△ACE; ③ △CDE为等边三角形,其中正确的结论是 ( )
②△ACD≌△ACE; ③ △CDE为等边三角形,其中正确的结论是 ( ) 
 厘米,并在点B、M处固定,则B、M之间的距离是多少?
厘米,并在点B、M处固定,则B、M之间的距离是多少?