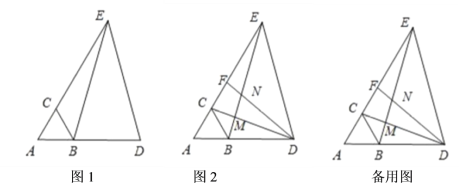
题目内容
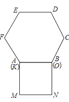
【题目】如图,在等边![]() 中,延长
中,延长![]() 至点
至点![]() ,延长
,延长![]() 交
交![]() 的中垂线于点
的中垂线于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,连接![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() 直接写出线段
直接写出线段![]() ,
,![]() ,
,![]() 的等量关系
的等量关系
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)过点![]() 作
作![]() 于点
于点![]() ,分别求出BH,BE,根据勾股定理问题得解;
,分别求出BH,BE,根据勾股定理问题得解;
(2)如图在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ,再证明
,再证明![]() ,问题得证;
,问题得证;
(3)过点![]() 作
作![]() 的垂线,构造出一个
的垂线,构造出一个![]() ,
,![]() ,
,![]() 的三角形和一个等腰直角三角形,借助(2)的结论,设
的三角形和一个等腰直角三角形,借助(2)的结论,设![]() ,
,![]() ,通过解两个直角三角形,代换
,通过解两个直角三角形,代换![]() 和
和![]() 的关系,得出结论.
的关系,得出结论.
解:(1)如图,过点![]() 作
作![]() 于点
于点![]() ,
,
在等边![]() 中∵
中∵![]()
∴![]() ,
,![]() ,
,
∵点E在BD的垂直平分线上,
∴![]() ,
,
在![]() 中
中![]()
∴![]()
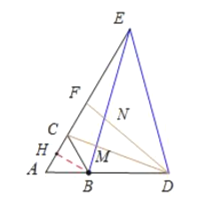
(2)如图在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]()
∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,
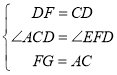
∴![]()
∴![]()
∴![]()
∴![]()
设![]()
∴![]()
在![]() 中
中
∴![]()
∴![]()
在![]() 和
和![]() 中
中
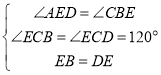
∴![]()
∴![]()
∴![]()
![]()
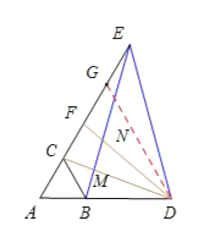
(3)如图,设![]() ,DP=y,
,DP=y,
过点![]() ⊥
⊥![]() ,垂足为P,
,垂足为P,
∵∠AED=45°, ∠A=60°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴BD=AD-AB=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】如图,漏壶是一种古代计时器.在它内部盛一定量的水,水从壶下的小孔漏出.壶内壁有刻度,人们根据壶中水面的位置计算时间.用x(小时)表示漏水时间,y(厘米)表示壶底到水面的高度,某次计时过程中,记录到部分数据如下表:
漏水时间x(小时) | … | 3 | 4 | 5 | 6 | … |
壶底到水面高度y(厘米) | … | 9 | 7 | 5 | 3 | … |
(1)问y与x的函数关系属于一次函数、二次函数和反比例函数中的哪一种?求出该函数解析式及自变量x的取值范围;
(2)求刚开始计时时壶底到水面的高度.