题目内容
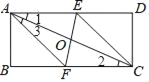
【题目】已知如图所示的一张平行四边形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
(1)求证:四边形AFCE是菱形.
(2)若AB=8cm,∠B=90°,△ABF的面积为24cm2,求菱形AFCE的周长.

【答案】(1)见解析;(2)菱形AFCE的周长为40cm.
【解析】试题分析: (1)由折叠可得EA=EC,FA=FC,∠2=∠3;由四边形ABCD为平行四边形可得∠1=∠2,根据等量代换可得∠1=∠3,由三线合一知△AEF为等腰三角形,所以AE=AF,从而可证四边形AFCE是菱形;
(2)由△ABF的面积为24cm2和AB=8cm,根据三角形面积公式可求出BF=6cm,利用勾股定理求出AF=10cm,从而可求出菱形的周长.
(1)证明:∵将平行四边形ABCD(AD>AB)折叠,使点A与点C重合,
∴EF垂直平分AC,
∴EA=EC,FA=FC,
∴∠2=∠3,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠1=∠2,
∴∠1=∠3,
∵AO⊥EF,
∴△AEF为等腰三角形,
∴AE=AF,
∴AE=EC=AF=CF,
∴四边形AFCE是菱形;
(2)解:在Rt△ABF中,∵![]() ABBF=24,AB=8cm,
ABBF=24,AB=8cm,
∴BF=6cm,
∴AB2+BF2=AF2=100,
∴AF=10cm,
∴菱形AFCE的周长为10×4=40(cm).
故菱形AFCE的周长为40cm.

练习册系列答案
相关题目
【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()



