题目内容
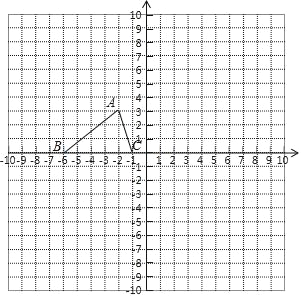
【题目】在平面直角坐标系xOy中,A(4,0),B(0,4),CD是△AOB的中位线.若将△COD绕点O旋转,得到△C′OD′,射线AC′与射线BD′的交点为P.
(1)∠APB的度数是_____°.
(2)在旋转过程中,记P点横坐标为m,则m的取值范围是_____.
【答案】90°; ![]()
【解析】
(1)由SAS证得△BOD'![]() △AOC',可得∠C'AO=∠D'BO,因为∠BMP=∠AMO,可得∠APB=∠AOB=90°;
△AOC',可得∠C'AO=∠D'BO,因为∠BMP=∠AMO,可得∠APB=∠AOB=90°;
(2)点P在AB为直径的⊙M上运动,过M作PM∥OA交⊙M于点P(在点M的左侧),此时m的值最小;当BD′与⊙O相切时,m最大,分别求出对应m的值,即可得出m的取值范围.
(1)如图1,
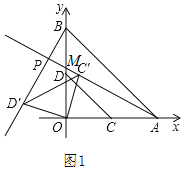
∵A(4,0),B(0,4),
∴OA=OB,∠AOB=90°,
∵CD是△AOB的中位线,
∴CO=DO=2=BD=AC,
∵将△COD绕点O旋转,得到△C′OD′,
∴CO=DO,∠C'OD'=90°=∠AOB,
∴∠BOD'=∠AOC',且C'O=D'O,AO=BO,
∴△BOD![]() △AOC'(SAS)
△AOC'(SAS)
∴∠C'AO=∠D'BO,
∵∠BMP=∠AMO,
∴∠APB=∠AOB=90°,
故答案为:90,
(2)如图2,
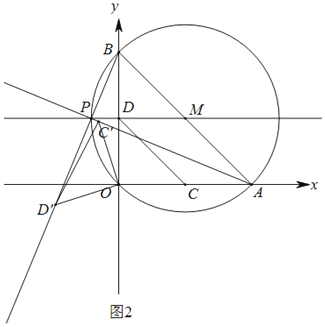
∵∠BPA=90°,
∴点P在AB为直径的⊙M上运动,
过M作PM∥OA交⊙M于点P(在点M的左侧),此时m的值最小,
∵AB=4![]() ,DM=2,
,DM=2,
∴PD=2![]() 2,
2,
∴m=22![]() .
.
如图3,
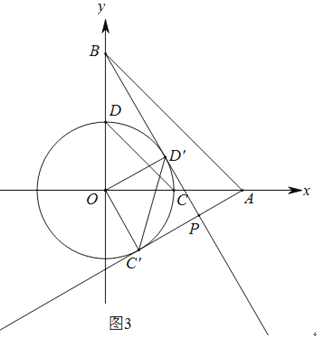
∵OD′=OC′=2,
∴点D′,点C′在⊙O上运动,
当BD′与⊙O相切时,m最大,
此时BD′=![]() ,D′P=OC′=2,
,D′P=OC′=2,
∴BP=2![]() +2,
+2,
∵OB4,OD′=2,
∴sin∠OBD′=![]() ,
,
∴m=![]() BP=
BP=![]() +1,
+1,
∴22![]() ≤m≤
≤m≤

练习册系列答案
相关题目