题目内容
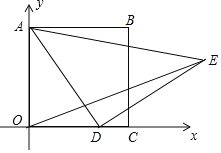
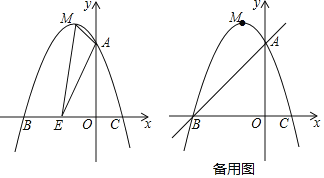
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() 在
在![]() 轴上,
轴上,![]() 是
是![]() 的中点,过点
的中点,过点![]() 的反比例函数图象交
的反比例函数图象交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() .
.
![]() 求过点
求过点![]() 的反比例函数的解析式及
的反比例函数的解析式及![]() 所在直线的函数解析式.
所在直线的函数解析式.
![]() 设直线
设直线![]() 与
与![]() 轴和
轴和![]() 轴的交点分别为
轴的交点分别为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() .反比例函数解析式为
.反比例函数解析式为![]() .直线的解析式为
.直线的解析式为![]() ,(2)9.
,(2)9.
【解析】
(1)根据勾股定理求出CD=4,得到D(4,3),即可求出反比例函数的解析式,根据D点的坐标求出点B,E的坐标即可求出结论;
(2)根据![]() 中直线DE的函数解析式,求出点
中直线DE的函数解析式,求出点![]() 的坐标即可求出
的坐标即可求出![]() 的面积.
的面积.
解:![]()
![]() 四边形
四边形![]() 为矩形.
为矩形.
![]() 为直角三角形.
为直角三角形.
![]() .
.
![]() .
.
![]() .
.
设反比例函数的解析式为![]() .
.
![]() 点
点![]() 在反比例函数图象上.
在反比例函数图象上.
![]() ,
,
![]() 反比例函数解析式为
反比例函数解析式为![]() .
.
![]() 为
为![]() 的中点,且
的中点,且![]() .
.
![]() ,
,
![]() 点的横坐标为
点的横坐标为![]() ,且
,且![]() 在反比例函数图象上.
在反比例函数图象上.
在![]() 中,令
中,令![]() ,得
,得![]() .
.
![]() ,
,
设![]() 所在直线的解析式为
所在直线的解析式为![]() .
.
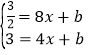 ,
,
![]() 直线的解析式为
直线的解析式为![]() ,
,
![]() 直线DE的解析式为
直线DE的解析式为![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() ,
,
![]() ,
,

练习册系列答案
相关题目