题目内容
阅读下列解题过程:题目:已知方程x2+mx+1=0的两个实数根是p、q,是否存在m的值,使得p、q满足
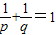 ?若存在,求出m的值;若不存在,请说明理由.
?若存在,求出m的值;若不存在,请说明理由.解:存在满足题意的m值.由一元二次方程的根与系数的关系得
p+q=m,pq=1.∴
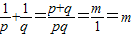 .∵
.∵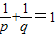 ,∴m=1.
,∴m=1.阅读后回答下列问题:上面的解题过程是否正确?若不正确,写出正确的解题过程.
【答案】分析:由两根之和=- ,算出m的值后,应根据根的判别式判断方程是否有根.
,算出m的值后,应根据根的判别式判断方程是否有根.
解答:解:不正确.
正确的解题过程如下:
不存在满足题意的m的值,理由是:
由一元二次方程的根与系数的关系得p+q=-m,pq=1.
∴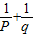 =
=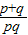 =
=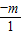 =-m.
=-m.
∵ =1.
=1.
∴m=-1.
当m=-1时,△=m2-4=-3<0,此时方程无实数根.
∴不存在满足题意的m的值.
点评:本题用到的知识点为:一元二次方程若有实数根,则两根之和=-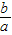 ,两根之积=
,两根之积=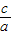 ;根的判别式小于0,原方程无解.
;根的判别式小于0,原方程无解.
 ,算出m的值后,应根据根的判别式判断方程是否有根.
,算出m的值后,应根据根的判别式判断方程是否有根.解答:解:不正确.
正确的解题过程如下:
不存在满足题意的m的值,理由是:
由一元二次方程的根与系数的关系得p+q=-m,pq=1.
∴
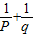 =
=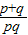 =
=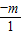 =-m.
=-m.∵
 =1.
=1.∴m=-1.
当m=-1时,△=m2-4=-3<0,此时方程无实数根.
∴不存在满足题意的m的值.
点评:本题用到的知识点为:一元二次方程若有实数根,则两根之和=-
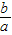 ,两根之积=
,两根之积=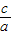 ;根的判别式小于0,原方程无解.
;根的判别式小于0,原方程无解. 
练习册系列答案
相关题目
 (体验探究题)阅读下列解题过程并填空.
(体验探究题)阅读下列解题过程并填空.