题目内容
【题目】已知,在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC.
(1)(特殊情况,探索结论)
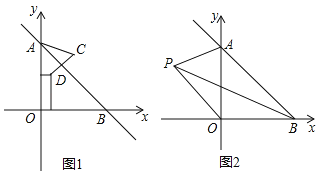
如图1,当点E为AB的中点时,确定线段AE与DB的大小关系,请你直接写出结论:
AE DB(填“>”、“<”或“=”).
(2)(特例启发,解答题目)
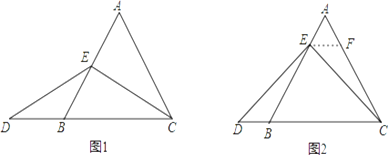
如图2,当点E为AB边上任意一点时,确定线段AE与DB的大小关系,请你直接写出结论,AE DB(填“>”、“<”或“=”);理由如下,过点E作EF∥BC,交AC于点F.(请你将解答过程完整写下来).
(3)(拓展结论,设计新题)
在等边三角形ABC中,点E在直线AB上,点D在线段CB的延长线上,且ED=EC,若△ABC的边长为1,AE=2,求CD的长.(请你画出相应图形,并直接写出结果).
【答案】(1)=;(2)=;理由见解析;(3)3.
【解析】
(1)由E为等边三角形AB边的中点,利用三线合一得到CE垂直于AB,且CE为角平分线,由ED=EC,利用等边对等角及等腰三角形的性质得到一对角相等,利用等角对等边即可得证;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,由三角形ABC为等边三角形,得到三角形AEF为等边三角形,进而得到AE=EF=AF,BE=FC,再由ED=EC,以及等式的性质得到夹角相等,利用SAS得到三角形BDE与三角形EFC全等,利用全等三角形对应边相等得到DB=EF,等量代换即可得证;
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,由BC+DB求出CD的长即可.
(1)当E为AB的中点时,AE=DB;
(2)AE=DB,理由如下,过点E作EF∥BC,交AC于点F,
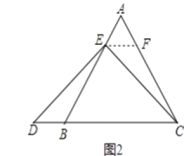
证明:∵△ABC为等边三角形,
∴△AEF为等边三角形,
∴AE=EF,BE=CF,
∵ED=EC,
∴∠D=∠ECD,
∵∠DEB=60°-∠D,∠ECF=60°-∠ECD,
∴∠DEB=∠ECF,
在△DBE和△EFC中,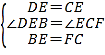 ,
,
∴△DBE≌△EFC(SAS),
∴DB=EF,
则AE=DB;
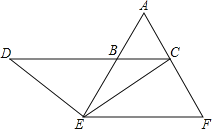
(3)点E在AB延长线上时,如图所示,同理可得△DBE≌△EFC,
∴DB=EF=2,BC=1,
则CD=BC+DB=3.
故答案为:(1)=;(2)=(3)3

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案