题目内容
【题目】在平面直角坐标系中,直线AB交y轴于A(0,a),交x轴于B(b,0),且a,b满足(a﹣b)2+|3a+5b﹣88|=0.
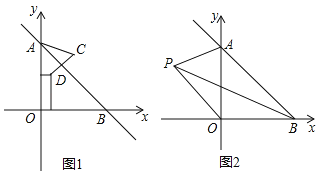
(1)求点A,B的坐标;
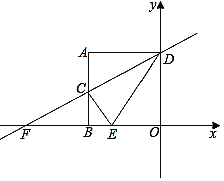
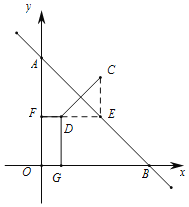
(2)如图1,已知点D(2,5),求点D关于直线AB对称的点C的坐标.
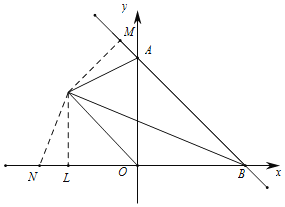
(3)如图2,若P是∠OBA的角平分线上的一点,∠APO=67.5°,求![]() 的值.
的值.
【答案】(1)A(0,11),B(11,0);(2)C的坐标为(6,9);(3)3
【解析】
(1)利用非负数的性质求出A、B两点坐标,再利用待定系数法切线直线AB解析式即可解决问题.
(2)延长FD交AB于点E,连结CE,易得△DEC,△AFE都是等腰直角三角形,再根据D(2,5),得到DG=5,进而得到AF=EF=6,最后得出C(6,9);
(3)利用角平分线的性质构造全等三角形,然后通过角度的关系得出边的关系即可.
解:(1)由题意得![]() ,
,
解得![]() ,
,
∴A(0,11),B(11,0);
(2)如图,延长FD交AB于点E,连结CE
因为OB=OA=11,
所以三角形OAB是等腰直角三角形,
易得△DEC,△AFE都是等腰直角三角形,
所以FE=AF=OA﹣OF=11﹣5=6,
∴CE=DE=EF﹣FD=6﹣2=4,
所以C的横坐标为6.,纵坐标为5+4=9,
故C的坐标为(6,9);
(3)如图,作PM垂直AB于点M,作PM垂直OB于点L,在L的左侧取一点N,使得NL=AM,
∵PB是∠ABO的平分线,
所以PM=PL,
∴△AMP≌△NLP,
∴∠NLP=∠APM,
∴∠APN=∠MPL.
∵∠ABO=45°,
∴∠MPL=135°,
∴∠APN=135°,
又∠APO=67.5°,
∴∠NPO=∠APO=67.5°.
∵PN=PA,PO=PO,
∴△OPN≌OPA,
∴∠PON=∠POA=45°,NO=AO=11,
设NL=a,则MA=a,
∴BL=BM=a+11![]() ,
,
∵BL=22﹣a,
∴22﹣a=a+11![]() ,
,
∴a=11﹣![]() ,
,
∴LO=11﹣(11﹣![]() )=
)=![]() ,
,
∴PO=![]() LO=11,
LO=11,
所以![]() =3.
=3.