题目内容
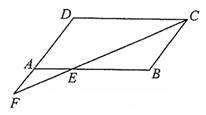
已知:如图, ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F。求证:AE=AF。
ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F。求证:AE=AF。
 ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F。求证:AE=AF。
ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F。求证:AE=AF。
证明:在平行四边形ABCD中,AB//DC,D//BC
∴∠AEF=∠DCE,∠F=∠BCE
∵CE平分∠DCB,∴∠DCE=∠BCE
∴∠F=∠AEF,
∴AE=AF
∴∠AEF=∠DCE,∠F=∠BCE
∵CE平分∠DCB,∴∠DCE=∠BCE
∴∠F=∠AEF,
∴AE=AF
利用平行四边形的性质可以推出AB∥DC,AD∥BC,然后利用它们得到角的关系,再利用角平分线即可证明题目结论

练习册系列答案
相关题目
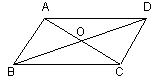

 比
比 大
大 .设
.设 ,
, ,那么
,那么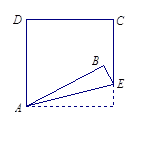




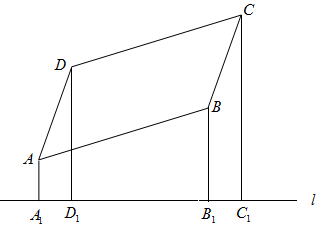
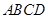 及四边形外一直线
及四边形外一直线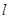 ,四个顶点
,四个顶点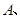
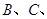
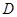 到直线
到直线 .
.

 中,
中, ,
, ,
,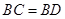 ,
, ,则
,则 ( )
( )



